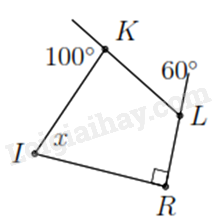
a) Tìm \(x\) trong hình vẽ bên.
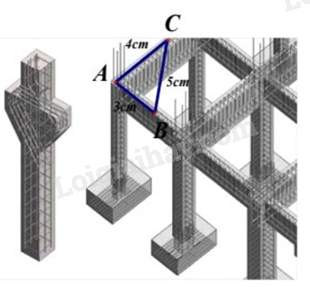
b) Khi xây móng nhà, để kiểm tra xem 2 phần móng có vuông góc với nhau hay không, người thợ xây thường lấy \(AB = 3cm,AC = 4cm\) (A là điểm chung của hai phần móng nhà hay còn gọi là góc nhà), rồi đo đoạn \(BC = 5cm\) thì hai phần móng đó vuông góc với nhau. Hãy giải thích vì sao?
a) Sử dụng định lí tổng các góc của một tứ giác là \(360^\circ \).
Góc trong và góc ngoài của một đỉnh có tổng là \(180^\circ \).
b) Sử dụng định lí Pythagore đảo để kiểm tra xem tam giác tạo thành có phải tam giác vuông không.
a) Vì góc ngoài tại \(K\) có số đo là \(100^\circ \) nên \(\widehat {IKL} = 180^\circ - 100^\circ = 80^\circ \).
Góc ngoài tại \(L\) có số đo là \(60^\circ \) nên \(\widehat {KLR} = 180^\circ - 60^\circ = 120^\circ \).
Ta có tổng các góc trong tứ giác là \(360^\circ \) nên \(\widehat {IKL} + \widehat {KLR} + \widehat {R\,} + \widehat {I\,} = 360^\circ \)
Suy ra \(80^\circ + 120^\circ + 90^\circ + x = 360^\circ \)
Do đó \(x = 70^\circ \).
b) Xét tam giác ABC có \(B{C^2} = {5^2} = 25\) và \(A{B^2} + A{C^2} = {3^2} + {4^2} = 25\)
Suy ra \(B{C^2} = A{B^2} + A{C^2}\).
Theo định lí Pythagore đảo, ta có \(\Delta ABC\) vuông tại A.
Vậy hai phần móng đó vuông góc với nhau.