Ba điểm A, B, C là ba điểm liên tiếp trên một sợi dây có — Không quảng cáo

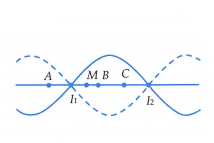
Theo bài ra vị trí của ba điểm A, B, C được thể hiện như hình vẽ.

Do biên độ của ba điểm A, B, C bằng nhau nên khoảng cách từ mỗi điểm này đến mỗi nút gần nó nhất phải bằng nhau. Ta có:

$\left\{ \begin{array}{l}A{I_1} = B{I_1} = C{I_2}\\AC = A{I_1} + {I_1}C = C{I_2} + {I_1}C = {I_1}{I_2} = \frac{\lambda }{2}\end{array} \right.$

Ta có: $AC = AB + BC = AB + \frac{{AB}}{2} = \frac{{3AB}}{2} = \frac{\lambda }{2} \Rightarrow \left\{ \begin{array}{l}AB = \frac{\lambda }{3}\\A{I_1} = \frac{\lambda }{6}\end{array} \right.$

Gọi ${A_{\rm{0}}} = 2a$ là biên độ tại bụng sóng, biên độ dao động tại điểm A là:

${A_A} = \left| {{A_{\rm{0}}}\sin 2\pi \frac{{\frac{\lambda }{6}}}{\lambda }} \right| = \left| {{A_{\rm{0}}}\sin \frac{\pi }{3}} \right| = \frac{{{A_{\rm{0}}}\sqrt 3 }}{2} = 4\sqrt 3  \Rightarrow {A_{\rm{0}}} = 8$

Khoảng cách từ M tới điểm nút I ₁ là: $M{I_1} = MA - {I_1}A = \frac{{AC}}{2} - {I_1}A = \frac{\lambda }{4} - \frac{\lambda }{6} = \frac{\lambda }{{12}}$

Biên độ dao động tại điểm M là: ${A_M} = \left| {{A_{\rm{0}}}\sin 2\pi \frac{{\frac{\lambda }{{12}}}}{\lambda }} \right| = \left| {{A_{\rm{0}}}\sin \frac{\pi }{6}} \right| = \frac{{{A_{\rm{0}}}}}{2} = 4cm$

Cứ sau những khoảng thời gian liên tiếp $\frac{T}{2}$ thì sợi dây duỗi thẳng.

Ta có: $\frac{T}{2} = {\rm{0}},25 \Rightarrow T = {\rm{0}},5 \Rightarrow \omega  = \frac{{2\pi }}{T} = 4\pi$

Tốc độ dao động cực đại của điểm M là: ${v_{M\max }} = {A_M}.\omega  = 4.4\pi  = 16\pi cm/s$

Đáp án C.