Ba lực cùng tác động vào một vật. Hai trong ba lực này hợp — Không quảng cáo

Sử dụng quy tắc tổng hợp lực.

Gọi $\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}}$ lần lượt là ba lực tác động vào vật đặt tại điểm O như hình.

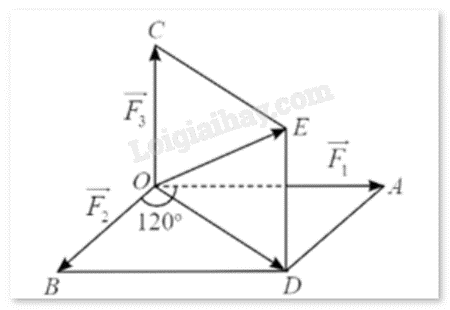
Ta có: $$\overrightarrow {{F_1}}  = OA,\overrightarrow {{F_2}}  = OB,\overrightarrow {{F_3}}  = OC$$ .

Khi đó, độ lớn các lực là OA = 25N, OB = 12N, OC = 4N.

Dựng hình bình hành OADB. Theo quy tắc hình bình hành, ta có: $\overrightarrow {OD}  = \overrightarrow {OA}  + \overrightarrow {OB}$.

Suy ra ${\overrightarrow {OD} ^2} = {\left( {\overrightarrow {OA}  + \overrightarrow {OB} } \right)^2} = {\overrightarrow {OA} ^2} + {\overrightarrow {OB} ^2} + 2\overrightarrow {OA} \overrightarrow {OB}$

$= O{A^2} + O{B^2} + 2OA.OB\cos \left( {\overrightarrow {OA} ,\overrightarrow {OB} } \right)$

$= {25^2} + {12^2} + 2.25.12\cos {120^o} = 469 = OD$.

Dựng hình bình hành ODEC.

Tổng lực tác động vào vật là $\overrightarrow F  = \overrightarrow {OE}  = \overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}$.

Độ lớn của hợp lực tác động vào vật là F = OE.

Vì OC⊥(OADC) nên OC⊥OD, suy ra ODEC là hình chữ nhật. Khi đó, tam giác ODE vuông tại D.

$O{E^2} = O{C^2} + O{D^2} = {4^2} + 469 = 485$.

Vậy $F = OE \approx 22$.