Bài 5.7 trang 141 SGK Toán 11 tập 1 - Cùng khám phá
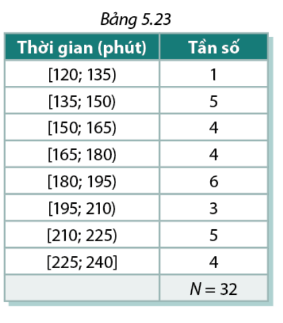
Bảng 5.23 biểu diễn kết quả thống kê về thời gian cần thiết để thực hiện cuộc chạy marathon đã được tổ chức ở một địa phương .
Đề bài
Bảng 5.23 biểu diễn kết quả thống kê về thời gian cần thiết để thực hiện cuộc chạy marathon đã được tổ chức ở một địa phương .
a, Xác định các tứ phân vị của mẫu số liệu
b, Xét nhóm gồm 50 % số cuộc thi có thời gian ngắn hơn đã được tổ chức. Thời gian tối đa của các cuộc thi trong nhóm này là bao nhiêu?

Phương pháp giải - Xem chi tiết
a, Sử dụng công thức tính các tứ phân vị
b, Thời gian tối đa của các cuộc thi trong nhóm này là \({Q_1}\)
Lời giải chi tiết
a, Bảng tần số tích lũy mẫu số liệu
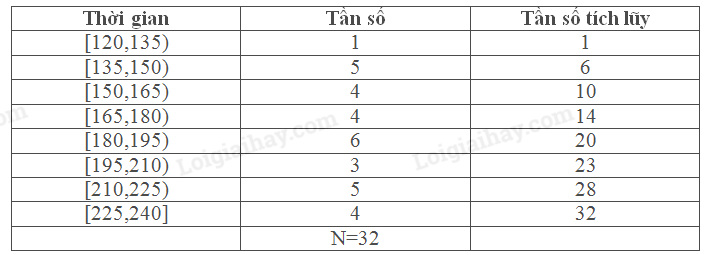
Ta có: \(\frac{N}{4} = \frac{{32}}{4} = 8 \Rightarrow \frac{N}{2} = 16 \Rightarrow \frac{{3N}}{4} = 24\)
Các nhóm chứa \({Q_1}\), \({Q_2}\) và \({Q_3}\) là [150,165), [180,195) và [210,225)
Độ dài các nhóm ghép đều là h=15
Ta có: \({L_1} = 150,{n_1} = 4,{T_1} = 6\)\( \Rightarrow {Q_1} = {L_1} + \frac{{\frac{N}{4} - {T_1}}}{{{n_1}}}.h = 150 + \frac{{8 - 6}}{4}.15 = 157,5\)
\({L_2} = 180,{n_2} = 6,{T_2} = 14\)\( \Rightarrow {Q_2} = {L_2} + \frac{{\frac{N}{2} - {T_2}}}{{{n_2}}}.h = 180 + \frac{{16 - 14}}{6}.15 = 185\)
\({L_3} = 210,{n_3} = 5,{T_3} = 23\)\( \Rightarrow {Q_3} = {L_3} + \frac{{\frac{{3N}}{4} - {T_3}}}{{{n_3}}}.h = 210 + \frac{{24 - 23}}{5}.15 = 213\)
b, Thời gian tối đa của các cuộc thi trong nhóm này là \({Q_1}\)=157,5 phút .