Bài tập 25 trang 123 Tài liệu dạy – học Toán 7 tập 2 — Không quảng cáo

Đề bài

Cho tam giác nhọn ABC và trực tâm H. Em hãy xác định trực tâm của các tam giác BCH, CHA, HAB.

Lời giải chi tiết

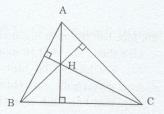
Ta có H là trực tâm của tam giác ABC (gt)

Nên \(CH \bot AB,BH \bot AC\) và \(AH \bot BC\)

∆BHC có: BA là đường cao (\(BA \bot CH\))

CA là đường cao (\(CA \bot BH\))

DA là đường cao (\(DA \bot BC\)) và BA, CA, DA cắt nhau tại A

Do đó A là trực tâm của ∆BHC

∆AHC có: BA là đường cao \((CH \bot AB)\)

BF là đường cao \((BF \bot AC)\)

BC là đường cao \((BC \bot AH)\)

BA, BF, BC cắt nhau tại B

Do đó B là trực tâm của ∆AHC.

∆ABH có: CA là đường cao \((CA \bot BH)\)

CE là đường cao \((CE \bot AB)\)

CB là đường cao \((CB \bot AH)\)

CA, CE, CB cắt nhau tại C

Do đó C là trực tâm của ∆ABH.