Bài tập cuối tuần Toán 4 tuần 27 - Đề 2 (Có đáp án và lời giải chi tiết)
Tải vềBài tập cuối tuần 27 - Đề 2 bao gồm các bài tập chọn lọc với các dạng bài tập giúp các em ôn lại kiến thức đã học trong tuần
Đề bài
Bài 1 . Chọn câu trả lời đúng
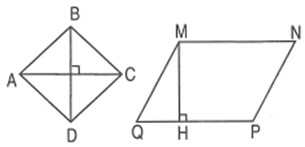
Hình thoi ABCD và hình bình hành MNPQ có AC = PQ, BD = MH
A. Diện tích hình thoi ABCD bằng diện tích hình bình hành MNPQ.
B. Diện tích hình thoi ABCD gấp 2 lần diện tích hình bình hành MNPQ.
C. Diện tích hình bình hành MNPQ gấp 2 lần diện tích hình thoi ABCD.
D. Diện tích hình thoi ABCD lớn hơn diện tích hình bình hành MNPQ.
Bài 2. Một hình thoi có đường chéo bé là 12cm và bằng \(\dfrac{3}{4}\) đường chéo lớn. Tính diện tích của hình thoi đó.
Bài giải
........................................................................................................................................
........................................................................................................................................
........................................................................................................................................
Bài 3. Một miếng kính hình thoi có diện tích là 210cm 2 . Biết độ dài đường chéo lớn là 28cm. Tính độ dài đường chéo bé.
Bài giải
........................................................................................................................................
........................................................................................................................................
........................................................................................................................................
Bài 4 . Hình chữ nhật EGHK có chiều dài và chiều rộng lần lượt bằng một nửa độ dài đường chéo dài và đường chéo ngắn của hình thoi ABCD. Tính tổng diện tích 4 hình tam giác AEG, BEK, CHK và DGH, biết diện tích hình thoi ABCD là 48cm 2 .

Bài giải
........................................................................................................................................
........................................................................................................................................
........................................................................................................................................
........................................................................................................................................
........................................................................................................................................
........................................................................................................................................
Lời giải chi tiết
Bài 1 .
Phương pháp:
Tính diện tích các hình theo các quy tắc:
- Tính diện tích hình thoi ta lấy tích độ dài hai đường chéo (cùng một đơn vị đo) chia cho 2.
- Tính diện tích hình bình hành ta lấy độ dài đáy nhân với chiều cao (cùng một đơn vị đo).
Cách giải:
Diện tích hình thoi ABCD là:
\(\dfrac{{BD \times AC}}{2}\) (1)
Diện tích hình bình hành MNPQ là:
\(MH \times PQ = BD \times AC\) (2)
Từ (1) và (2) ta suy ra diện tích hình bình hành MNPQ gấp 2 lần diện tích hình thoi ABCD.
Chọn đáp án C.
Bài 2 .
Phương pháp:
- Tính độ dài đường chéo lớn ta lấy độ dài đường chéo bé chia cho \(\dfrac{3}{4}\) hoặc lấy độ dài đường chéo bé chia cho 3 rồi nhân với 4.
- Tính diện tích hình thoi ta lấy tích độ dài hai đường chéo chia cho 2 (cùng một đơn vị đo).
Cách giải:
Độ dài đường chéo lớn là:
12 : \(\dfrac{3}{4}\) = 16 (cm)
Diện tích hình thoi đó là:
16 × 12 : 2 = 96 (cm 2 )
Đáp số: 96cm 2 .
Bài 3 .
Phương pháp:
Tính độ dài đường chéo bé ta lấy 2 lần diện tích chia cho độ dài đường chéo lớn.
Cách giải:
Độ dài đường chéo bé là:
210 × 2 : 28 = 15 (cm)
Đáp số: 15cm.
Bài 4 .
Phương pháp:
Tính diện tích các hình theo các quy tắc:
- Tính diện tích hình thoi ta lấy tích độ dài hai đường chéo (cùng một đơn vị đo) chia cho 2.
- Tính diện tích hình chữ nhật ta lấy chiều dài nhân với chiều rộng (cùng một đơn vị đo).
Cách giải:
Gọi độ dài đường chéo lớn là a, độ dài đường chéo bé là b.
Diện tích hình thoi ABCD là:
\(\dfrac{{{\rm{a\;}} \times {\rm{b}}}}{2}\) (1)
Theo đề bài ta có: ciều dài hình chữ nhật là \(\dfrac{{\rm{a}}}{2}\), chiều rộng hình chữ nhật là \(\dfrac{{\rm{b}}}{2}\).
Diện tích hình chữ nhật EGHK là:
\(\dfrac{a}{2} \times \dfrac{b}{2} = \dfrac{{{\rm{a\;}} \times {\rm{b}}}}{4} = \dfrac{{{\rm{a\;}} \times {\rm{b}}}}{2} \times \dfrac{1}{2}\) (2)
Từ (1) và (2) ta suy ra diện tích diện tích hình chữ nhật EGHK bằng \(\dfrac{1}{2}\) diện tích hình thoi ABCD , hay hình thoi ABCD gấp 2 lần diện tích hình chữ nhật EGHK.
Diện tích hình chữ nhật EGHK là:
48 : 2 = 24 (cm 2 )
Tổng diện tích 4 hình tam giác là:
48 – 24 = 24 (cm 2 )
Đáp số: 24cm 2 .