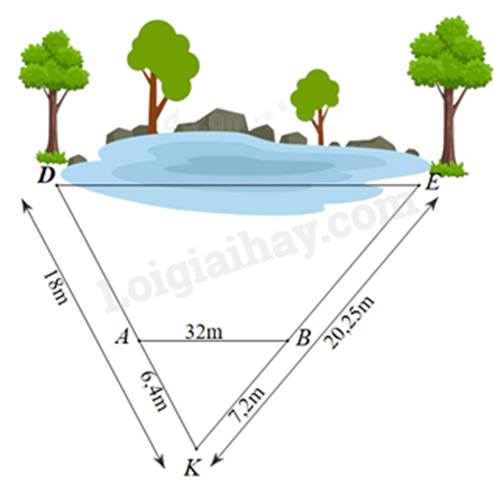
Bạn An đo được khoảng cách từ vị trí mình đứng (điểm K) đến cây D và cây E ở hai bên hồ nước lần lượt là KD = 18m và KE = 20,25m. Để tính độ dài DE, An xác định điểm A nằm giữa K, D và điểm E nằm giữa K, E sao cho KA = 6,4m, KB = 7,2m và khoảng cách giữa A và B là 32m.
a) Chứng minh \(\frac{{KB}}{{KE}} = \frac{{AK}}{{AD}}\).
b) Chứng minh \(AB//DE\).
c) Tính khoảng cách giữa D và E.
a) Dựa vào tỉ số hai đoạn thẳng để chứng minh.
b) Dựa vào định lí Thales đảo để chứng minh.
c) Áp dụng hệ quả của định lí Thales để suy ra tỉ số giữa AB và DE để tính DE.
a) Ta có:
\(\begin{array}{l}\frac{{KB}}{{KE}} = \frac{{7,2}}{{20,25}} = \frac{{16}}{{45}}\\\frac{{KA}}{{KD}} = \frac{{6,4}}{{18}} = \frac{{16}}{{45}}\end{array}\)
\( \Rightarrow \frac{{KB}}{{KE}} = \frac{{KA}}{{KD}}\) (đpcm)
b) Vì \(\frac{{KB}}{{KE}} = \frac{{KA}}{{KD}}\) (cmt) nên AB // DE (Định lí Thales đảo trong tam giác)
c) Vì AB // DE nên ta có:
\(\begin{array}{l}\frac{{AB}}{{DE}} = \frac{{KA}}{{KD}} = \frac{{16}}{{45}}\\\frac{{32}}{{DE}} = \frac{{16}}{{45}}\\ \Rightarrow DE = 32:\frac{{16}}{{45}} = 90\left( m \right)\end{array}\)
Vậy khoảng cách giữa D và E là 90m.