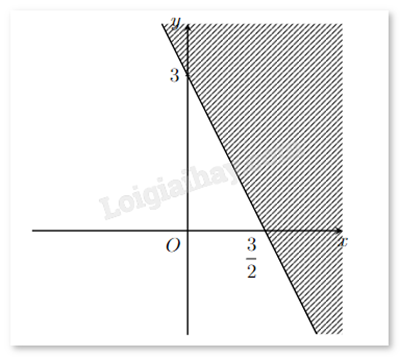
Biểu diễn hình học miền nghiệm không tô màu của bất phương — Không quảng cáo

Tìm phương trình đường thẳng bờ của miền nghiệm. Thay tọa độ một điểm bất kì vào phương trình đường thẳng vừa tìm để xác định chiều của bất đẳng thức.

Gọi đường thẳng bờ của miền nghiệm là d, có dạng $y = cx + d$.

Vì điểm (0;3) và $\left( {\frac{3}{2};0} \right)$ thuộc d nên ta có hệ:

$\left\{ {\begin{array}{*{20}{c}}{3 = 0c + d}\\{0 = \frac{3}{2}c + d}\end{array}} \right.$ hay $\left\{ {\begin{array}{*{20}{c}}{d = 3}\\{c =  - 2}\end{array}} \right.$

Vậy d: $y =  - 2x + 3$ hay $2x + y = 3$.

Thay điểm O(0;0) vào phương trình d, ta được: 2.0 + 0 = 0 < 3.

Quan sát hình vẽ thấy O thuộc miền nghiệm nên bất phương trình cần tìm là $2x + y \le 3$.

Suy ra a = 2, b = 1. Vậy a + b = 2 + 1 = 3.