1. Chiếc hộp (Hình a) được vẽ lại như Hình b có dạng hình chóp tam giác đều S.MNP.
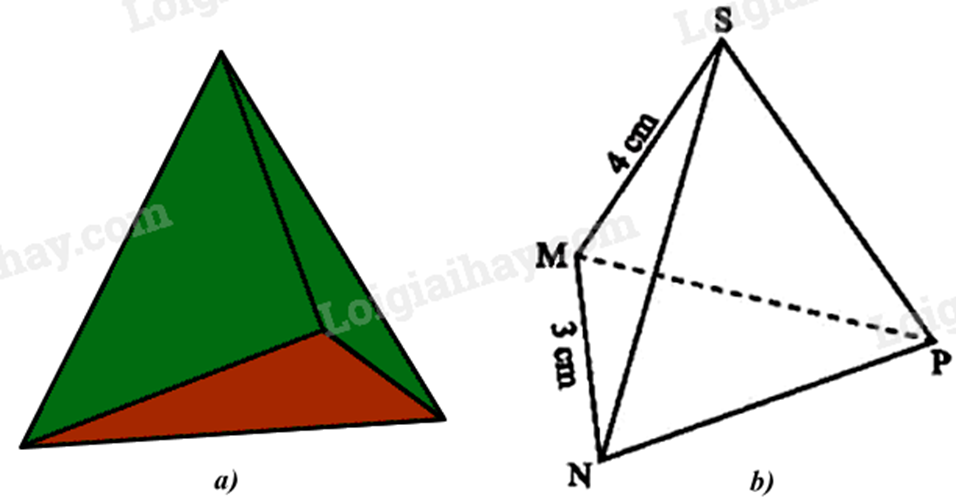
a) Hãy cho biết mặt đáy, mặt bên, cạnh bên của chiếc hộp đó.
b) Cho biết SM = 4cm, MN = 3 cm. Tìm độ dài các cạnh còn lại của chiếc hộp.
2. Người ta làm mô hình một kim tự tháp ở cổng vào của bảo tàng Louvre. Mô hình có dạng hình chóp tứ giác đều, chiều cao 21 m, độ dài cạnh đáy là 34 m.

a) Cạnh bên của hình chóp là bao nhiêu?
b) Tính thể tích hình chóp.
1. Dựa vào đặc điểm của hình chóp tam giác đều để xác định.
2. a) Sử dụng định lí Pythagore vào tam giác vuông để tính cạnh bên của hình chóp.
b) Sử dụng công thức tính thể tích hình chóp tứ giác đều: \(V = S.h\) (S là diện tích đáy, h là chiều cao).
1.
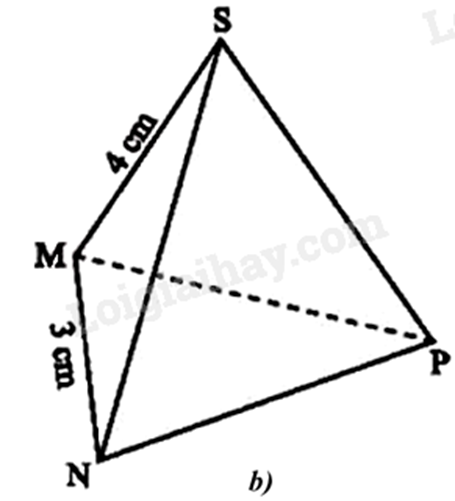
a) Mặt đáy là: (MNP).
Các mặt bên là: (SMN), (SNP), (SMP).
Các cạnh bên là: SM, SN, SP.
b) Độ dài các cạnh còn lại của chiếc hộp là:
SN = SP = SM = 4cm;
NP = MP = MN = 3cm.
2.
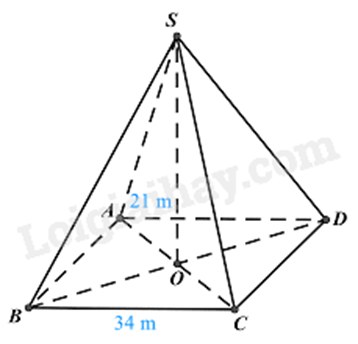
Giả sử kim tự tháp Lu-vrơ (Louvre) là hình chóp tứ giác đều S.ABCD.
Hình chóp tứ giác đều S.ABCD có ABCD là hình vuông nên AC = BD nên AO = OB.
Áp dụng định lí Pythagore vào tam giác vuông AOB, ta có:
\(\begin{array}{l}A{O^2} + O{B^2} = A{B^2}\\2A{O^2} = {34^2}\\A{O^2} = {34^2}:2 = 1156:2 = 578\end{array}\)
Vì S.ABCD là hình chóp tứ giác đều nên \(SO \bot AO\), suy ra \(\Delta SAO\) vuông tại O.
Áp dụng định lí Pythagore vào tam giác vuông SAO, ta có:
\(S{A^2} = S{O^2} + A{O^2} = {21^2} + 578 = 1019\).
Suy ra \(SA = \sqrt {1019} \approx 31,9\left( m \right)\).
b) Thể tích kim tự tháp là:
\(V = \frac{1}{3}{.34^2}.21 = 8092\left( {{m^3}} \right)\).