Cho \(A = \frac{{x + 1}}{{x - 2}} + \frac{{x - 1}}{{x + 2}} + \frac{{{x^2} + 4x}}{{4 - {x^2}}}\) với \(x \ne \pm 2.\)
a) Rút gọn biểu thức \(A\).
b) Tính giá trị của \(A\) khi \(x = 4\).
c) Tìm giá trị nguyên của \(x\) để \(A\) nhận giá trị nguyên dương.
a) Quy đồng mẫu thức để rút gọn biểu thức.
b) Thay \(x = 4\) vào \(A\) để tính giá trị.
c) Ta biến đổi để đưa A về dạng \(A = m + \frac{a}{B}\) với m và a là số nguyên.
Khi đó A có giá trị nguyên khi \(a \vdots B\) hay \(B \in \) Ư(a).
a) Với \(x \ne \pm 2\), ta có:
\(A = \frac{{x + 1}}{{x - 2}} + \frac{{x - 1}}{{x + 2}} + \frac{{{x^2} + 4x}}{{4 - {x^2}}}\)
\( = \frac{{x + 1}}{{x - 2}} + \frac{{x - 1}}{{x + 2}} - \frac{{{x^2} + 4x}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}\)
\( = \frac{{\left( {x + 1} \right)\left( {x + 2} \right)}}{{\left( {x - 2} \right)\left( {x + 2} \right)}} + \frac{{\left( {x - 1} \right)\left( {x - 2} \right)}}{{\left( {x - 2} \right)\left( {x + 2} \right)}} - \frac{{{x^2} + 4x}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}\)
\( = \frac{{{x^2} + 3x + 2 + {x^2} - 3x + 2 - {x^2} - 4x}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}\)
\( = \frac{{{x^2} - 4x + 4}}{{\left( {x - 2} \right)\left( {x + 2} \right)}} = \frac{{{{\left( {x - 2} \right)}^2}}}{{\left( {x - 2} \right)\left( {x + 2} \right)}} = \frac{{x - 2}}{{x + 2}}\).
Vậy với \(x \ne \pm 2\) ta có \(A = \frac{{x - 2}}{{x + 2}}.\)
b) Thay \(x = 4\) (thỏa mãn) vào biểu thức \(A\) ta có: \(A = \frac{{4 - 2}}{{4 + 2}} = \frac{2}{6} = \frac{1}{3}.\)
c) Với \(x \ne \pm 2\) và \(x \in \mathbb{Z}\) ta có: \(A = \frac{{x - 2}}{{x + 2}} = \frac{{x + 2 - 4}}{{x + 2}} = 1 - \frac{4}{{x + 2}}\)
Ta có \(1 \in \mathbb{Z}\) nên để \(A = 1 - \frac{4}{{x + 2}}\) nhận giá trị nguyên thì \(\frac{4}{{x + 2}} \in \mathbb{Z}\),
suy ra \(4 \vdots \left( {x + 2} \right)\)
hay \(\left( {x + 2} \right) \in \)Ư\(\left( 4 \right) = \left\{ { \pm 1; \pm 2; \pm 4} \right\}\)
Ta có bảng sau:
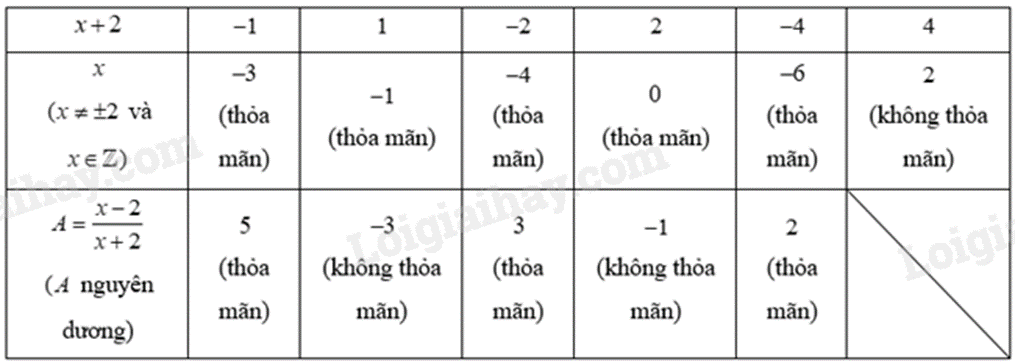
Vậy \(x \in \left\{ { - 3; - 4; - 6} \right\}.\)