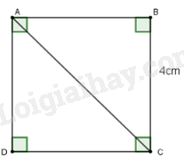
Cho ABCD là hình vuông cạnh 4 cm hình vẽ. Khi đó độ dài — Không quảng cáo

Phương pháp giải

Áp dụng định lí Pythagore: Trong một tam giác vuông, bình phương hai cạnh huyền bằng tổng bình phương hai cạnh góc vuông.

Vì ABCD là hình vuông nên AB = AC = 4cm

Áp dụng định lý Pythagore: Trong một tam giác vuông, bình phương hai cạnh huyền bằng tổng bình phương hai cạnh góc vuông. cho tam giác ABC vuông tại B ta có

$A{C^2} = A{B^2} + B{C^2} = {4^2} + {4^2} = 32 \Rightarrow AC = \sqrt {32} = 4\sqrt 2 cm$