Cho ba số thực dương a, b, c khác 1. Đồ thị các hàm số \(y = {\log _a}x,y = {\log _b}x,y = {\log _c}x\) thể hiện ở hình vẽ dưới đây.
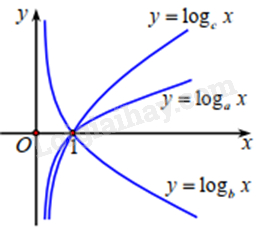
Khẳng định nào dưới đây là đúng?
-
A.
\(b < c < a\).
-
B.
\(b < a < c\).
-
C.
\(a < b < c\).
-
D.
\(a < c < b\).
Nếu \(0 < a < 1\) thì hàm số \(y = {\log _a}x\left( {a > 0,a \ne 1} \right)\) nghịch biến trên \(\left( {0; + \infty } \right)\).
Nếu \(a > 1\) thì hàm số \(y = {\log _a}x\left( {a > 0,a \ne 1} \right)\) đồng biến trên \(\left( {0; + \infty } \right)\).
Ta thấy hàm số \(y = {\log _b}x\) nghịch biến trên \(\left( {0; + \infty } \right)\) nên \(b < 1\).
Hàm số \(y = {\log _a}x,y = {\log _c}x\) đồng biến trên \(\left( {0; + \infty } \right)\) nên \(a > 1,c > 1\).
Xét tại một điểm \(x > 1\) thì: \({\log _c}x > {\log _a}x \Rightarrow {\log _c}x > \frac{1}{{{{\log }_x}a}} \Rightarrow {\log _c}x.{\log _x}a > 1 \Rightarrow a > c\)
Do đó, \(b < c < a\).
Đáp án A.
Đáp án : A