Cho biểu thức \(A = \left( {\frac{1}{{x - 2}} - \frac{{2x}}{{4 - {x^2}}} + \frac{1}{{2 + x}}} \right).\left( {\frac{2}{x} - 1} \right)\)
a) Rút gọn A.
b) Tính giá trị của biểu thức A tại x thỏa mãn: \({x^2} + 3x = 0\).
c) Tìm x để \(A = \frac{1}{2}\).
d) Tìm x nguyên để A nguyên dương.
a) Tìm điều kiện để các phân thức xác định. Sử dụng các quy tắc tính với phân thức đại số để rút gọn A.
b) Tìm x thỏa mãn \({x^2} + 3x = 0\). Thay x vừa tìm được để tính giá trị của A.
c) Thay \(A = \frac{1}{2}\) để tìm x.
d) Để A nguyên dương thì tử thức phải chia hết cho mẫu thức, tử thức và mẫu thức phải cùng dấu.
a) ĐKXĐ: \(\left\{ \begin{array}{l}x - 2 \ne 0\\4 - {x^2} \ne 0\\2 + x \ne 0\\x \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne 2\\x \ne - 2\\x \ne 0\end{array} \right.\)
Ta có: \(A = \left( {\frac{1}{{x - 2}} - \frac{{2x}}{{4 - {x^2}}} + \frac{1}{{2 + x}}} \right).\left( {\frac{2}{x} - 1} \right)\)
\(\begin{array}{l} = \left( {\frac{1}{{x - 2}} + \frac{{2x}}{{{x^2} - 4}} + \frac{1}{{x + 2}}} \right).\left( {\frac{{2 - x}}{x}} \right)\\ = \left( {\frac{{x + 2}}{{\left( {x - 2} \right)\left( {x + 2} \right)}} + \frac{{2x}}{{\left( {x - 2} \right)\left( {x + 2} \right)}} + \frac{{x - 2}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}} \right).\left( {\frac{{2 - x}}{x}} \right)\\ = \frac{{x + 2 + 2x + x - 2}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}.\frac{{2 - x}}{x}\\ = \frac{{4x}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}.\frac{{2 - x}}{x}\\ = \frac{{ - 4}}{{x + 2}}\end{array}\)
Vậy \(A = \frac{{ - 4}}{{x + 2}}\).
b) Ta có: \({x^2} + 3x = 0\)
\(\begin{array}{l}x\left( {x + 3} \right) = 0\\\left[ \begin{array}{l}x = 0\,\left( L \right)\\x = - 3\,\left( {TM} \right)\end{array} \right.\end{array}\)
Thay \(x = - 3\) vào A, ta được:
\(A = \frac{{ - 4}}{{ - 3 + 2}} = \frac{{ - 4}}{{ - 1}} = 4\)
Vậy \(A = 4\) tại x thỏa mãn: \({x^2} + 3x = 0\).
c) Để \(A = \frac{1}{2}\) thì \(\frac{{ - 4}}{{x + 2}} = \frac{1}{2}\)
\(\begin{array}{l} \Rightarrow - 4.2 = x + 2\\x + 2 = - 8\\x = - 10\end{array}\)
Vậy \(x = - 10\) thì \(A = \frac{1}{2}\).
d) Đề A nguyên dương thì \(\frac{{ - 4}}{{x + 2}}\) nguyên dương \( \Rightarrow - 4 \vdots \left( {x + 2} \right)\) và \(x + 2 < 0\) hay \(\left( {x + 2} \right) \in \) Ước nguyên âm của -4.
Mà Ước âm của -4 là: \(\left\{ { - 1; - 2; - 4} \right\}\)
Ta có bảng giá trị sau:
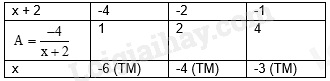
Vậy các giá trị của x để A nguyên dương là: \(x \in \left\{ { - 6; - 4; - 3} \right\}\).