Cho d1: Y = m - 1/2x - M - 5 và d2: Y = m + 3x - 2m + 7 a Tìm — Không quảng cáo

Phương pháp giải

a) Dựa vào kiến thức về vị trí tương đối của hai đường thẳng:

Hai đường thẳng $y = ax + b$ và $y = a'x + b'$ song song với nhau khi và chỉ khi $\left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right.$.

b) Thay m vào $\left( {{d_1}} \right)$ và $\left( {{d_2}} \right)$. Lấy hai điểm thuộc đồ thị hàm số để vẽ.

a) Để $\left( {{d_1}} \right)//\left( {{d_2}} \right)$ thì:

$\begin{array}{l}\left\{ \begin{array}{l}\frac{{m - 1}}{2} = m + 3\\ - m - 5 \ne  - 2m + 7\end{array} \right.\\\left\{ \begin{array}{l}m - 1 = 2m + 6\\m \ne 12\end{array} \right.\\\left\{ \begin{array}{l}m =  - 7\\m \ne 12\end{array} \right.\end{array}$

Vậy m = -7 thì $\left( {{d_1}} \right)//\left( {{d_2}} \right)$.

b) Thay m = -7 vào $\left( {{d_1}} \right)$ và $\left( {{d_2}} \right)$, ta được:

$\left( {{d_1}} \right):y = \frac{{ - 7 - 1}}{2}x - \left( { - 7} \right) - 5 =  - 4x + 2$

$\left( {{d_2}} \right):y = \left( { - 7 + 3} \right)x - 2.\left( { - 7} \right) + 7 =  - 4x + 21$

Vẽ $\left( {{d_1}} \right):y =  - 4x + 2$

+ Cho x = 0 thì y = -4.0 + 2 = 2. Ta được điểm A(0; 2).

+ Cho y = 0 thì 0 = -4x + 2 => x =$\frac{1}{2}$. Ta được điểm $B\left( {\frac{1}{2};0} \right)$.

Đường thẳng AB chính là đường thẳng $\left( {{d_1}} \right)$.

Vẽ $\left( {{d_2}} \right):y =  - 4x + 21$

+ Cho x = 0 thì y = -4.0 + 21 = 21. Ta được điểm C(0; 21).

+ Cho y = 0 thì 0 = -4x + 21 => x =$\frac{{21}}{4}$. Ta được điểm $D\left( {\frac{{21}}{4};0} \right)$.

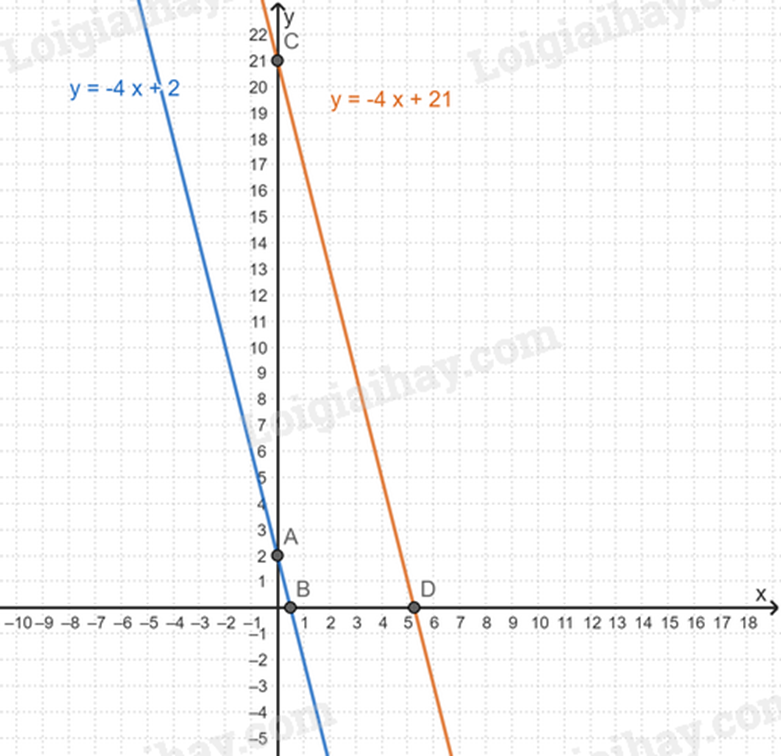
Đường thẳng CD chính là đường thẳng $\left( {{d_2}} \right)$.

Ta có $\left( {{d_1}} \right)$ và $\left( {{d_2}} \right)$ như sau: