Cho \(\left( {{d_1}} \right):y = x - 4\) và \(\left( {{d_2}} \right):y = - 3x + 2\).
a) Vẽ \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) trên cùng một hệ trục tọa độ.
b) Tìm tọa độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\).
c) Tìm m để \(\left( {{d_3}} \right):y = \left( {m - 2} \right)x + 3m + 12\) đi qua giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\).
a) Lấy hai điểm thuộc hàm số để vẽ đồ thị hàm số.
b) Giải phương trình hoành độ giao điểm của hai đường thẳng để tìm tọa độ giao điểm.
c) Thay tọa độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) vào \(\left( {{d_3}} \right)\) để tìm m.
a) Vẽ \(\left( {{d_1}} \right):y = x - 4\)
+ Cho x = 0 thì y = 0 – 4 = -4. Ta được điểm A(0; -4).
+ Cho y = 0 thì 0 = x – 4 => x = 4. Ta được điểm B(4; 0).
Đường thẳng AB chính là đường thẳng \(\left( {{d_1}} \right)\).
Vẽ \(\left( {{d_2}} \right):y = - 3x + 2\)
+ Cho \(x = 0\) thì \(y = - 3.0 + 2 = 2\). Ta được điểm \(C\left( {0;2} \right)\).
+ Cho \(y = 0\) thì \(0 = - 3x + 2 \Rightarrow x = \frac{2}{3}\). Ta được điểm \(D\left( {\frac{2}{3};0} \right)\).
Đường thẳng CD chính là đường thẳng \(\left( {{d_1}} \right)\).
Ta có đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\):
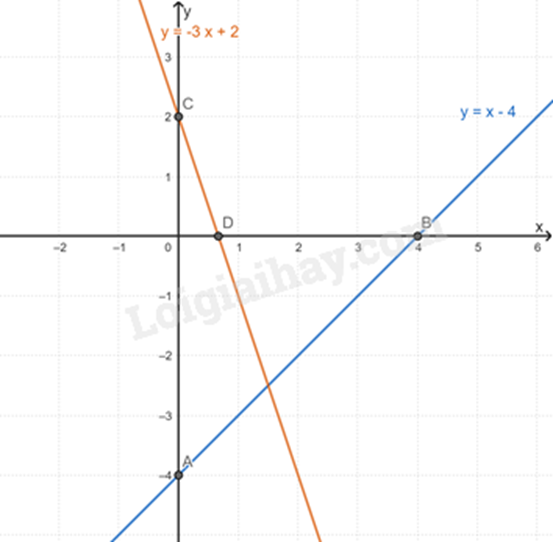
b) Phương trình hoành độ giao điểm của hai đường thẳng là:
\(\begin{array}{l}x - 4 = - 3x + 2\\x + 3x = 2 + 4\\4x = 6\\x = \frac{3}{2}\end{array}\)
\( \Rightarrow y = \frac{3}{2} - 4 = - \frac{5}{2}\).
Vậy tọa độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) là \(E\left( {\frac{3}{2};\frac{{ - 5}}{2}} \right)\).
c) Vì \(\left( {{d_3}} \right)\) đi qua tọa độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) nên \(E\left( {\frac{3}{2};\frac{{ - 5}}{2}} \right) \in \left( {{d_3}} \right)\).
Thay tọa độ điểm E vào hàm số \(y = \left( {m - 2} \right)x + 3m + 12\), ta được:
\(\begin{array}{l}\frac{{ - 5}}{2} = \left( {m - 2} \right).\frac{3}{2} + 3m + 12\\\frac{{ - 5}}{2} = \frac{3}{2}m - 3 + 3m + 12\\\frac{9}{2}m = - \frac{{23}}{2}\\ \Rightarrow m = - \frac{{23}}{9}\end{array}\)
Vậy \(m = \frac{{ - 23}}{9}\) thì \(\left( {{d_3}} \right):y = \left( {m - 2} \right)x + 3m + 12\) đi qua giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\).