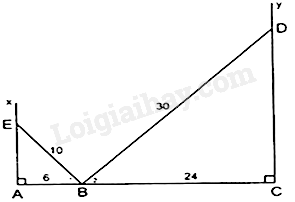
Cho điểm B nằm trên đoạn thẳng AC sao cho AB = 6cm,BC = — Không quảng cáo

Phương pháp giải

Sử dụng kiến thức trường hợp đồng dạng thứ nhất của tam giác vuông: Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác kia thì hai tam giác vuông đó đồng dạng với nhau.

Áp dụng định lý Pythagore vào tam giác CDB vuông ở C ta có:

$B{D^2} = D{C^2} + C{B^2}$

$D{C^2} = {30^2} - {24^2} = 324 \Rightarrow DC = 18cm$

Xét tam giác BEA và tam giác DBC có:

$\widehat A = \widehat C = {90^0},\frac{{BE}}{{BD}} = \frac{{BA}}{{DC}}\left( { = \frac{1}{3}} \right)$

Do đó, $\Delta BEA \backsim \Delta DBC$, suy ra $\widehat {EBA} = \widehat {BDC}$

Mà $\widehat {DBC} + \widehat {BDC} = {90^0} \Rightarrow \widehat {DBC} + \widehat {EBA} = {90^0}$

Lại có: $\widehat {DBC} + \widehat {EBD} + \widehat {EBA} = {180^0}$ nên $\widehat {EBD} = {90^0}$

Do đó, tam giác BDE vuông tại B.

Diện tích tam giác EBD là : $\frac{1}{2}BE.BD = \frac{1}{2}.10.30 = 150\left( {c{m^2}} \right)$

Áp dụng định lý Pythagore vào tam giác EBD vuông tại B có:

$E{D^2} = E{B^2} + B{D^2} = {10^2} + {30^2} = 1000 \Rightarrow ED = \sqrt {1000} cm$

Chu vi tam giác EBD là: $EB + BD + ED = 10 + 30 + \sqrt {1000}  = 40 + \sqrt {1000} \left( {cm} \right)$

Vậy có 1 khẳng định đúng.