Cho đoạn thẳng $AB$ và điểm $M$ nằm giữa $A$ và $B$$;MA — Không quảng cáo

Phương pháp giải

Áp dụng tính chất tam giác vuông cân, tính chất đường cao của tam giác.

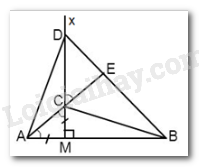
Vì $Mx \bot AB \Rightarrow \widehat {AMx} = {90^0}$

Xét $\Delta AMC$ có $\left\{ \begin{array}{l}\widehat {AMC} = {90^0}\left( {cmt} \right)\\MA = MC\left( {gt} \right)\end{array} \right.$ $\Rightarrow \widehat {MAC} = \widehat {MCA} = {45^0}$ (tính chất tam giác vuông cân)

Do đó $\widehat {DCE} = \widehat {MCA} = {45^0}$ (đối đỉnh)

Xét $\Delta BMD$ có: $\left\{ \begin{array}{l}\widehat {BMD} = {90^0}\left( {cmt} \right)\\MB = MD\left( {gt} \right)\end{array} \right.$ $\Rightarrow \widehat {MBD} = \widehat {MDB} = {45^0}$(tính chất tam giác vuông cân)

Xét $\Delta CDE$ có: $\widehat {CDE} = \widehat {DCE} = {45^0}$ $\Rightarrow \widehat {CDE} + \widehat {DCE} = {90^0} \Rightarrow \widehat {DEC} = {90^0}.$

Lại có: $\widehat {DEC} + \widehat {AEB} = {180^0}$ (kề bù) $\Rightarrow \widehat {AEB} = {180^0} - \widehat {DEC} = {180^0} - {90^0} = {90^0}$ .