Cho đường thẳng d: Y = - 2x - 4. Gọi A, B lần lượt là giao — Không quảng cáo

Phương pháp giải

+ Bước 1: Tìm tọa độ giao điểm A, B

+ Bước 2: Sử dụng công thức tính diện tích tam giác AOB vuông tại O: $S = \frac{{OA.OB}}{2}$

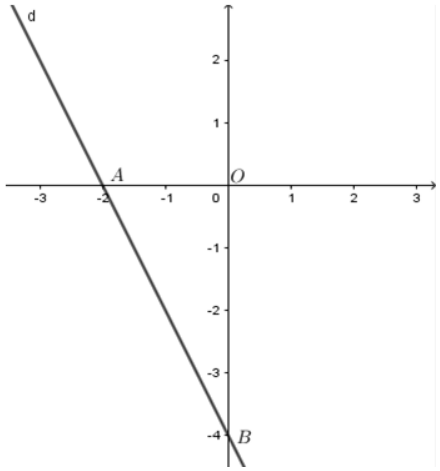
A là giao điểm của d với trục hoành nên $0 =  - 2x - 4,x =  - 2$ nên $A\left( { - 2;0} \right)$

B là giao điểm của d với trục tung nên $y =  - 2.0 - 4 =  - 4$ nên $B\left( {0; - 4} \right)$

Do đó, $OA = 2,OB = 4$

Vì tam giác AOB vuông tại O nên diện tích tam giác OAB là: $S = \frac{{OA.OB}}{2} = \frac{{2.4}}{2} = 4$ (đvdt)