Cho G là trọng tâm của tam giác đều. Chọn câu — Không quảng cáo

Phương pháp giải

- Xét các tam giác bằng nhau, suy ra các cạnh tương ứng bằng nhau.

- Áp dụng tính chất đường trung tuyến của tam giác.

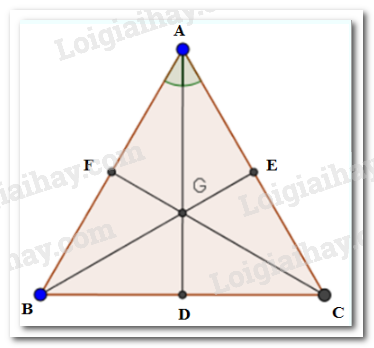
Các tia $AG,BG$ và $CG$  cắt $BC,AC,AB$ lần lượt tại $D,E,F$ thì $D,E,F$ theo thứ tự là trung điểm của $BC,AC,AB.$

Mà   $BC = AC = AB$ (do tam giác $ABC$ là tam giác đều), do đó $BD = DC = CE = EA = AF = FB$

Xét \(\Delta AEB\) và \(\Delta AFC\) ta có:  $AB = AC;$ \(\widehat A\) chung; $AE = AF.$

Vậy \(\Delta AEB = AFC\,(c.g.c)\), suy ra $BE = CF\,\,\,\,\left( 1 \right)$

Chứng minh tương tự ta có \(\Delta BEC = ADC\,(c.g.c)\), suy ra $BE = AD\left( 2 \right)$

Từ (1) và (2) ta có:  $AD = BE = CF\left( 3 \right)$

Theo đề bài $G$  là trọng tâm của tam giác $ABC$  nên ta có:

\(GA = \dfrac{2}{3}AD;\,\,GB = \dfrac{2}{3}BE;\,\,GC = \dfrac{2}{3}CF\)

Vì thế từ (3) ta suy ra $GA = GB = GC.$