Cho góc nhọn xOy. Trên tia Ox lấy hai điểm A,C, trên tia — Không quảng cáo

Phương pháp giải

+ Sử dụng tính chất hai tam giác bằng nhau ở ý trước suy ra hai góc tương ứng bằng nhau

+ Sau đó sử dụng tính chất hai góc kề bù hoặc góc ngoài để so sánh hai góc $\widehat {CAD}$ và $\widehat {CBD}.$

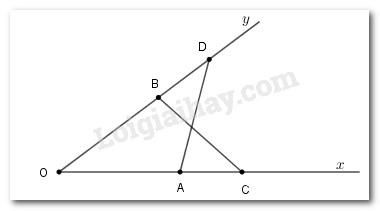
Xét tam giác $OAD$ và tam giác $OBC$ có

$OA = OB,$

$\widehat O$chung,

$OC = OD$

$\Rightarrow$$\Delta OAD = \Delta OBC$ ( c.g.c)

$\Rightarrow$$\widehat {OBC} = \widehat {OAD}$ (hai góc tương ứng bằng nhau)

Lại có $\widehat {OBC} + \widehat {CBD} = 180^\circ ;\,\widehat {OAD} + \widehat {DAC} = 180^\circ$ (hai góc kề bù)

Nên $\widehat {CBD} = 180^\circ  - \widehat {OBC}$ và $\widehat {CAD} = 180^\circ  - \widehat {OAD}$  mà $\widehat {OBC} = \widehat {OAD}$ (cmt)

$\Rightarrow$ $\widehat {CBD} = \widehat {CAD}.$