Cho góc \(xAy\) khác góc bẹt. Trên tia Ax lấy các điểm \({\rm{B}},{\rm{C}}\). Qua \({\rm{B}},{\rm{C}}\) vẽ 2 đường thẳng song song cắt \(Ay\) lần lượt ở \(D\) và \(E\). Qua \(E\) vẽ đường thẳng song song với \(CD\) cắt tia \(Ax\) ở \(F\).
a) So sánh \(\frac{{AB}}{{AC}}\) và \(\frac{{AD}}{{AE}};\frac{{AC}}{{AF}}\) và \(\frac{{AD}}{{AE}}\)
b) CMR: \(A{C^2} = AB \cdot AF\)
a) Áp dụng định lí Thales để so sánh tỉ số các cặp cạnh đã cho.
b) Áp dụng tính chất bắc cầu để suy ra biểu thức cần chứng minh.
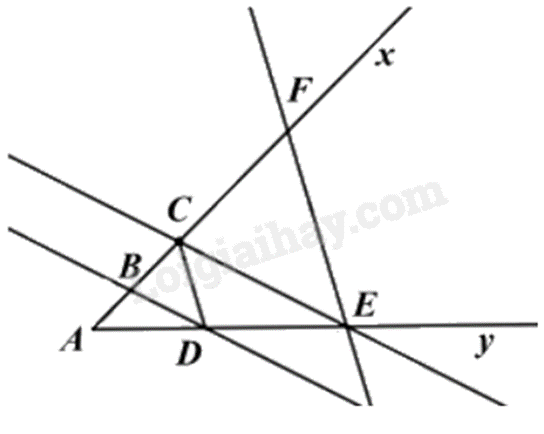
a) Vì \({\rm{BD}}//{\rm{CE}}\), áp dụng định lý Talet ta có: \(\frac{{AB}}{{AC}} = \frac{{AD}}{{AE}}\)
Vì \({\rm{CD}}//{\rm{EF}}\), áp dụng định lý Talet ta có: \(\frac{{AC}}{{AF}} = \frac{{AD}}{{AE}}\)
b) Từ (1) và (2) ta có:
\(\frac{{AB}}{{AC}} = \frac{{AC}}{{AF}}\) suy ra \(AC \cdot AC = AB \cdot AF\) hay \(A{C^2} = AB \cdot AF\) (điều phải chứng minh)