Cho hai hàm số bậc nhất : \({d_1}\): y = 2x - 3 và \({d_2}\): y = x – 2 .
a) Vẽ đồ thị các hàm số trên cùng một mặt phẳng tọa độ Oxy.
b) Tìm tọa độ giao điểm của hai đồ thị hàm số trên.
c) Xác định a, b của hàm số bậc nhất y = ax + b, (a \( \ne \) 0) biết rằng đồ thị hàm số \({d_3}\) của hàm số y = ax + b song song với \({d_1}\) và cắt đường thẳng \({d_2}\) tại B có hoành độ bằng -1.
a) Lấy hai điểm thuộc đồ thị hàm số, đồ thị hàm số là đường thẳng đi qua hai điểm đó.
b) Viết phương trình hoành độ giao điểm hai đồ thị hàm số đó để tìm giao điểm.
c) Dựa vào vị trí tương đối của hai đường thẳng để xác định a. Thay tọa độ điểm B vào hàm số để tìm b.
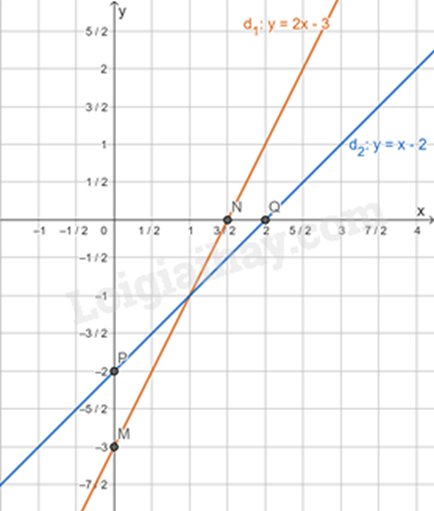
a) +) Với hàm số \(y = 2x - 3\):
Cho x = 0 thì y = -3.
Cho y = 0 thì x = \(\frac{3}{2}\).
Đồ thị của hàm số \(y = 2x - 3\) là đường thẳng đi qua hai điểm \(M\left( {0; - 3} \right)\) và \(N\left( {\frac{3}{2};0} \right)\).
+) Với hàm số \(y = x - 2\):
Cho x = 0 thì y = -2.
Cho y = 0 thì x = 2.
Đồ thị của hàm số \(y = x - 2\) là đường thẳng đi qua hai điểm \(P\left( {0; - 2} \right)\) và \(Q\left( {2;0} \right)\).
Ta có đồ thị của hai hàm số:
b) Xét phương trình hoành độ giao điểm của hai đồ thị hàm số y = 2x – 3 và y = x – 2, ta có:
\(\begin{array}{l}2x - 3 = x - 2\\2x - x = - 2 + 3\\x = 1\\ \Rightarrow y = 1 - 2 = - 1\end{array}\)
Vậy tọa độ giao điểm của hai đồ thị hai hàm số là A(1; -1).
c) Ta có \({d_3}//{d_1} \Rightarrow y = 2x + b\)
Vì \({d_1}\) cắt đường thẳng \({d_2}\) tại B có hoành độ bằng -1 \( \Rightarrow B\left( { - 1;0} \right) \in {d_3}\)
\( \Rightarrow 0 = 2.\left( { - 1} \right) + b \Rightarrow b = 2\)
Vậy hàm số cần tìm là \(y = 2x + 2\).