Cho hai hình chữ nhật ABCD và A’B’C’D’ thỏa mãn AC = — Không quảng cáo

Phương pháp giải

Sử dụng kiến thức trường hợp đồng dạng thứ nhất của tam giác vuông: Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác kia thì hai tam giác vuông đó đồng dạng với nhau.

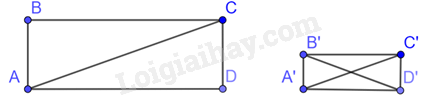
Vì \(AC = 3AB \Rightarrow \frac{{AB}}{{AC}} = \frac{1}{3},B'D' = 3A'B' \Rightarrow \frac{{A'B'}}{{B'D'}} = \frac{1}{3}\)

Do đó, \(\frac{{AB}}{{AC}} = \frac{{A'B'}}{{B'D'}} \Rightarrow \frac{{AB}}{{A'B'}} = \frac{{AC}}{{B'D'}}\)

Tam giác ABC và tam giác A’B’D’ có:

\(\widehat {ABC} = \widehat {B'A'D'} = {90^0};\frac{{AB}}{{A'B'}} = \frac{{AC}}{{B'D'}}\) nên \(\Delta ABC \backsim B'A'D'\left( 1 \right)\)

Chứng minh được \(\Delta B'A'D' = \Delta A'B'C'\left( 2 \right)\)

Từ (1) và (2) ta có: \(\Delta ABC \backsim \Delta A'B'C'\)

Do đó, \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}} = \frac{1}{2}\)

Diện tích hình chữ nhật ABCD là: \({S_{ABCD}} = AB.BC\)

Diện tích hình chữ nhật A’B’C’D’ là: \({S _{A'B'C'D'}} = A'B'.B'C'\)

Do đó: \(\frac{{{S_{ABCD}}}}{{{S_{A'B'C'D'}}}} = \frac{{AB.BC}}{{A'B'.B'C'}} = \frac{{AB}}{{A'B'}}.\frac{{BC}}{{B'C'}} = 2.2 = 4\)

\( \Rightarrow {S_{A'B'C'D'}} = \frac{{12}}{4} = 3\left( {c{m^2}} \right)\)