Cho hai hình vuông EFGH, E’F’G’H’ lần lượt có độ dài cạnh — Không quảng cáo

+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H ₁ đồng dạng phối cảnh với hình H và bằng hình H’

+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H

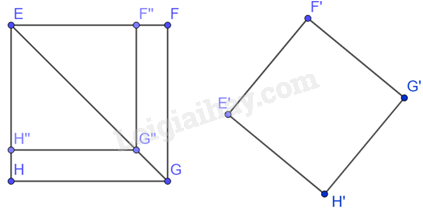
Trên các đoạn thẳng EF, EG, EH, ta lần lượt lấy các điểm F”, G”, H” sao cho \(\frac{EF''}{EF}=\frac{EG''}{EG}=\frac{EH''}{EH}=\frac{4}{5}.\) Theo định lý Thalès đảo ta có: F”G”//FG, G”H”//GH.

Mà \(\widehat{F''EH''}={{90}^{0}}\) nên tứ giác EF”G”H” là hình chữ nhật.

Mặt khác, ta có: \(\frac{EF''}{EF}=\frac{F''G''}{FG}=\frac{G''H''}{GH}=\frac{H''E}{HE}=\frac{4}{5}\) (hệ quả định lí Thalès)

Suy ra \(EF''=F''G''=G''H''=H''E=8cm\) .

Do đó, tứ giác EF”G”H” là hình vuông có độ dài cạnh bằng 8cm.

Suy ra, hai hình vuông EF”G”H” và E’F’G’H’ bằng nhau

Vì \(\frac{EF''}{EF}=\frac{EG''}{EG}=\frac{EH''}{EH}=\frac{4}{5}\) nên hình vuông EF”G”H” đồng dạng phối cảnh với hình vuông EFGH hay hình vuông E’F’G’H’ đồng dạng phối cảnh với hình vuông EFGH .

Vậy hình vuông E’F’G’H’ đồng dạng với hình vuông EFGH.