Cho hàm số có bảng biến thiên như hình vẽ sau.
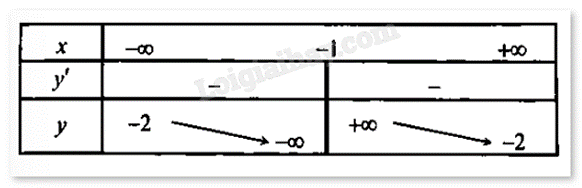
Xác định công thức của hàm số.
-
A.
\(y = \frac{{x - 4}}{{2x + 2}}\)
-
B.
\(y = \frac{{ - 2x - 4}}{{x + 1}}\)
-
C.
\(y = \frac{{ - 2x + 3}}{{x + 1}}\)
-
D.
\(y = \frac{{2 - x}}{{x + 1}}\)
Dựa vào sự biến thiên, tiệm cận và các điểm hàm số đi qua để lập hệ phương trình tìm hệ số.
Đồ thị hàm số có tiệm cận đứng x = -1 và tiệm cận ngang y = -2. Loại A và D.
Xét hàm số \(y = \frac{{ - 2x - 4}}{{x + 1}}\) có \(y' = \frac{2}{{{{(x + 1)}^2}}} > 0\). Hàm số đồng biến trên các khoảng xác định của nó.
Xét hàm số \(y = \frac{{ - 2x + 3}}{{x + 1}}\) có \(y' = \frac{{ - 5}}{{{{(x + 1)}^2}}} < 0\). Hàm số nghịch biến trên các khoảng xác định của nó.
Mà theo bảng biến thiên thì hàm số nghịch biến. Ta chọn hàm số \(y = \frac{{ - 2x + 3}}{{x + 1}}\).
Đáp án : C