Cho hàm số e^x - 2x + 3 — Không quảng cáo

a) Hàm số đã cho nghịch biến trên R

b) Hàm số đã cho đạt cực tiểu tại x = ln2

c) Đồ thị hàm số cắt trục tung tại điểm có tọa độ (0;4)

d) Đồ thị hàm số đã cho không đi qua gốc tọa độ

Lập bảng biến thiên và nhận xét.

Tập xác định: $D = \mathbb{R}$.

$y' = {e^x} - 2$.

Ta có $y' = 0 \Leftrightarrow {e^x} - 2 = 0 \Leftrightarrow x = \ln 2$.

Ta có bảng biến thiên:

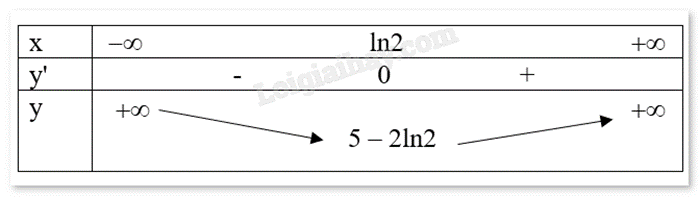
a) Sai. Hàm số f(x) nghịch biên trên $( - \infty ;\ln 2)$ và đồng biến trên $(\ln 2; + \infty )$.

b) Đúng. Hàm số đã cho đạt cực tiểu tại x = ln2.

c) Đúng. Vì khi x = 0 thì y = 4, đồ thị đi qua điểm có tọa độ (0;4).

d) Đúng. Vì gốc tọa độ O(0;0) thay vào hàm số thấy không thỏa mãn.