Cho hàm số \(f(x) = a{x^3} + b{x^2} + cx + d\) có bảng biến thiên như hình vẽ:
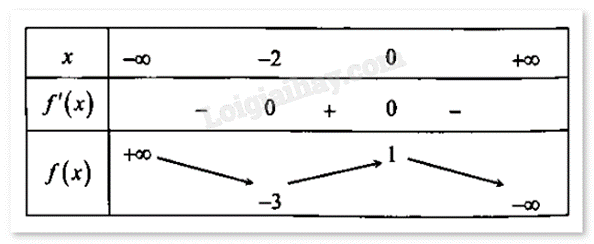
Xác định công thức của hàm số.
-
A.
\(y = {x^3} - 3{x^2} + 1\)
-
B.
\(y = - {x^3} - 3{x^2} + 1\)
-
C.
\(y = {x^3} - 3{x^2} + 2\)
-
D.
\(y = - {x^3} - 3{x^2} - 1\)
Quan sát bảng biến thiên, tìm đạo hàm, xét các điểm cực trị và các giá trị của hàm số tại điểm đó, thay số vào f(x), f’(x) để tìm các hệ số của phương trình.
Ta có: \(f'(x) = 3a{x^2} + 2bx + c\). Đồ thị đạt cực trị tại các điểm (0;1) và (-2;-3) nên f’(0) = 0, f’(-2) = 0.
Đồ thị hàm số đi qua các điểm (-2;-3) và (0;1) nên f(-2) = -3, f(0) = 1.
Ta có hệ phương trình sau:
\(\left\{ {\begin{array}{*{20}{c}}{f'(0) = 0}\\{f(0) = 1}\\{f'( - 2) = 0}\\{f( - 2) = - 3}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{c = 0}\\{d = 1}\\{12a - 4b = 0}\\{ - 8a + 4b + 1 = - 3}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{c = 0}\\{d = 1}\\{a = - 1}\\{b = - 3}\end{array}} \right.\)
Vậy hàm số cần tìm là: \(y = - {x^3} - 3{x^2} + 1\).
Đáp án : B