Cho hàm số \(f(x) = {x^3} - 24x\).
a) Hàm số f(x) đồng biến trên khoảng \(( - \infty ;0)\)
b) Đồ thị hàm số có điểm cực tiểu là (16;-2048)
c) Hàm số f(x) có giá trị lớn nhất trên đoạn [2;19] bằng 6403
d) Hàm số f(x) có giá trị nhỏ nhất trên đoạn [2;19] bằng -40
a) Hàm số f(x) đồng biến trên khoảng \(( - \infty ;0)\)
b) Đồ thị hàm số có điểm cực tiểu là (16;-2048)
c) Hàm số f(x) có giá trị lớn nhất trên đoạn [2;19] bằng 6403
d) Hàm số f(x) có giá trị nhỏ nhất trên đoạn [2;19] bằng -40
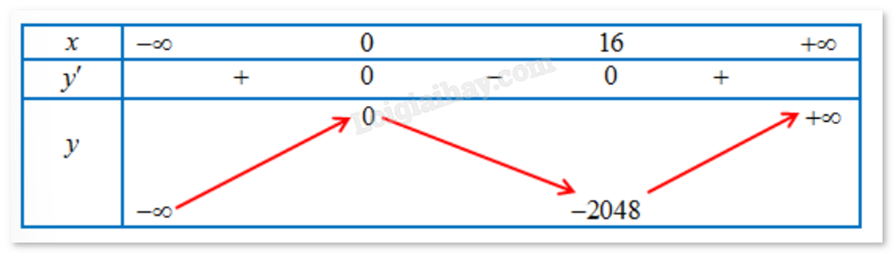
Lập bảng biến thiên và nhận xét.
\(f'(x) = 3{x^2} - 24 = 0 \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 2\sqrt 2 \in [2;19]}\\{x = - 2\sqrt 2 \notin [2;19]}\end{array}} \right.\)
f(2) = 40; \(f(2\sqrt 2 ) = - 32\sqrt 2 \); f(19) = 6403.
a) Sai. Hàm số f(x) nghịch biến trên \((0;16)\) và đồng biến trên \((16; + \infty )\).
b) Đúng. Đồ thị hàm số có điểm cực tiểu là (16;-2048).
c) Đúng. Hàm số f(x) có giá trị lớn nhất trên [-1;2] bằng 6403.
d) Sai. Hàm số f(x) có giá trị nhỏ nhất trên [-1;2] bằng \( - 32\sqrt 2 \).