Cho hàm số \(f(x) = - {x^4} + 12{x^2} + 1\).
a) Hàm số f(x) đồng biến trên khoảng (1;37)
b) Số điểm cực trị của hàm số đã cho là 3
c) Hàm số f(x) có giá trị nhỏ nhất trên đoạn [-1;2] bằng 12
d) Hàm số f(x) có giá trị lớn nhất trên đoạn [-1;2] bằng 33
a) Hàm số f(x) đồng biến trên khoảng (1;37)
b) Số điểm cực trị của hàm số đã cho là 3
c) Hàm số f(x) có giá trị nhỏ nhất trên đoạn [-1;2] bằng 12
d) Hàm số f(x) có giá trị lớn nhất trên đoạn [-1;2] bằng 33
Lập bảng biến thiên và nhận xét.
\(f'(x) = - 4{x^3} + 24{x^2} = 0\) khi \(x = \sqrt 6 \), \(x = - \sqrt 6 \) hoặc x = 0.
Bảng biến thiên:
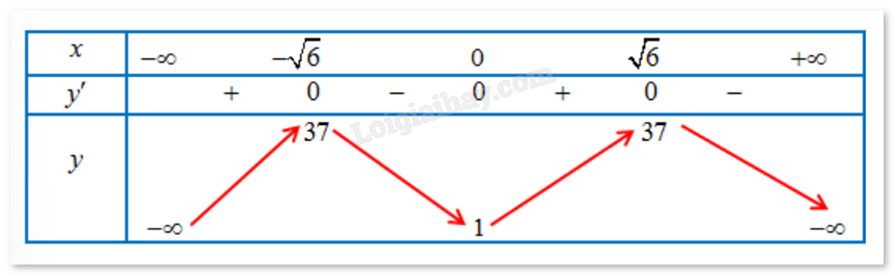
Ta có: f(-1) = 12; f(2) = 33; f(0) = 1.
a) Sai. Hàm số f(x) nghịch biến trên .
b) Đúng. Hàm số có ba điểm cực trị (, x = 0, ).
c) Sai. Hàm số f(x) có giá trị nhỏ nhất trên [-1;2] bằng 1.
d) Đúng. Hàm số f(x) có giá trị lớn nhất trên [-1;2] bằng 33.