Đề bài
Con hãy điền từ / cụm từ/ số thích hợp vào các ô trống
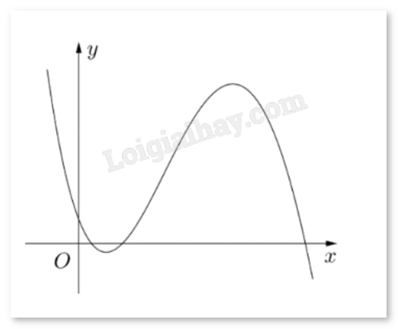
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) \((a,b,c,d \in \mathbb{R})\) có đồ thị là đường cong như hình bên. Có bao nhiêu số dương trong các số \(a,b,c,d\)?
Đáp án:
Đáp án
Đáp án:
Phương pháp giải
Quan sát đồ thị và nhận xét.
Quan sát đồ thị, thấy: \(\mathop {\lim }\limits_{x \to + \infty } y = - \infty \) suy ra \(a < 0\).
Gọi \({x_1},{x_2}\) lần lượt là hai điểm cực trị của hàm số đã cho \(({x_1} < {x_2})\).
Quan sát đồ thị, thấy \({x_1} + {x_2} > 0\) nên \(ab < 0\). Mà a < 0 suy ra b > 0.
Quan sát đồ thị, thấy \({x_1}.{x_2} > 0\) nên \(ac > 0\). Mà a < 0 suy ra c < 0.
Đồ thị hàm số giao trục tung tại điểm có tung độ \(d\) nằm phía trên trục hoành suy ra \(d > 0\).
Vậy, trong các số \(a,b,c,d\) có hai số \(b,d\) dương.