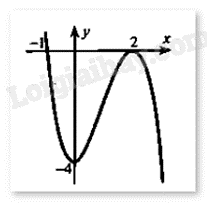
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) có bảng biến thiên như hình vẽ sau:
-
A.
\(y = {x^3} + 3{x^2} - 4\)
-
B.
\(y = - {x^3} + 3{x^2} + 4\)
-
C.
\(y = {x^3} + 3{x^2} + 4\)
-
D.
\(y = - {x^3} + 3{x^2} - 4\)
Dựa vào sự biến thiên, cực trị và các điểm hàm số đi qua để lập hệ phương trình tìm hệ số.
Ta có: \(f'(x) = 3a{x^2} + 2bx + c\).
Đồ thị hàm số đạt cực trị tại điểm (0;-4) và (2;0) nên ta có:
\(\left\{ {\begin{array}{*{20}{c}}{f'(0) = 0}\\{f(0) = - 4}\\{f'(2) = 0}\\{f(2) = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{c = 0}\\{d = - 4}\\{12a + 4b + c = 0}\\{8a + 4b + 2c + d = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{3a + b = 0}\\{2a + b = 1}\\{c = 0}\\{d = - 4}\end{array}} \right.} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = - 1}\\{b = 3}\\{c = 0}\\{d = - 4}\end{array}} \right.\)
Vậy hàm số cần tìm là \(y = - {x^3} + 3{x^2} - 4\).
Đáp án : D