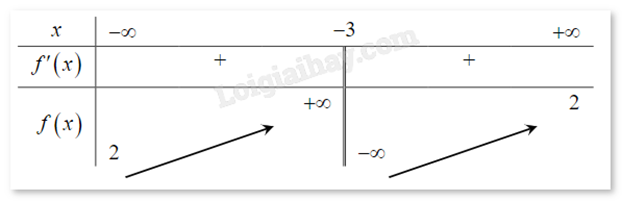
Cho hàm số y = ax + b/cx + d có bảng biến thiên như hình vẽ — Không quảng cáo

Phương pháp giải

Quan sát bảng biến thiên và nhận xét.

Dựa vào bảng biến thiên ta thấy đồ thị nhận x = -3 là tiệm cận đứng và y = 2 là tiệm cận ngang. Loại A, B.

Hàm số đồng biến trên mỗi khoảng xác định.

Xét hàm số $y = \frac{{2x + 7}}{{x + 3}} \Rightarrow y' = \frac{{ - 1}}{{{{(x + 3)}^2}}} < 0$ $(\forall x \ne  - 3)$, ta loại đáp án C.