Đề bài
Con hãy điền từ / cụm từ/ số thích hợp vào các ô trống
Cho hàm số y = f(x) có đồ thị như hình:
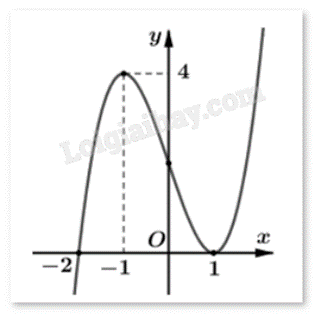
Tìm số điểm cực trị của hàm số \(g(x) = f({x^2} - 3)\).
Đáp án:
Đáp án
Đáp án:
Phương pháp giải
Tìm số nghiệm bội lẻ của phương trình g’(x) = 0.
Ta có: \(g'(x) = [f({x^2} - 3)]' = ({x^2} - 3)'f'({x^2} - 3) = 2xf'({x^2} - 3)\).
\(g'(x) = 0 \Leftrightarrow \left[ {\begin{array}{{20}{c}}{2x = 0}\\{f'({x^2} - 3) = 0}\end{array} \Leftrightarrow \left[ {\begin{array}{{20}{c}}{x = 0}\\{{x^2} - 3 = - 2}\\{{x^2} - 3 = 1}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{{20}{c}}{x = 0}\\{x = \pm 1}\\{x = \pm 2}\end{array}} \right.} \right.\)
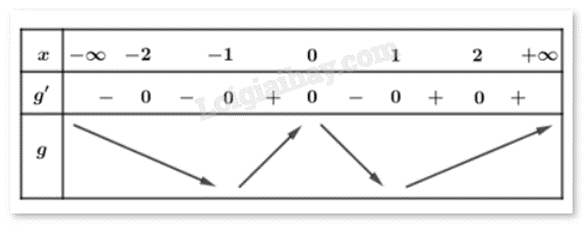
Vì f’(x) không đổi dấu khi qua x = 1 nên g(x) có 3 điểm cực trị.