Cho hệ trục tọa độ Oxy, diện tích của hình chữ nhật giới — Không quảng cáo

Phương pháp giải

Sử dụng định nghĩa tọa độ của điểm trong mặt phẳng: Cho điểm M trong mặt phẳng tọa độ Oxy, giả sử hình chiếu của điểm M lên trục hoành Ox là điểm a trên trục số Ox, hình chiếu của điểm M lên trục tung Oy là điểm b trên trục số Oy. Cặp số (a; b) được gọi là tọa độ của điểm M, a là hoành độ, b là tung độ của điểm M

+ Sử dụng khái niệm đồ thị của hàm số: Đồ thị của hàm số \(y = f\left( x \right)\) trên mặt phẳng tọa độ Oxy là tập hợp tất cả các điểm \(M\left( {x;f\left( x \right)} \right)\)

Các điểm có hoành độ bằng 3 nằm trên đường thẳng song song với trục tung và cắt trục hoành tại điểm có hoành độ bằng 3.

Các điểm có tung độ bằng 2 nằm trên đường thẳng song song với trục hoành và cắt trục tung tại điểm có tung độ bằng 2.

Do đó, ta có đồ thị hàm số:

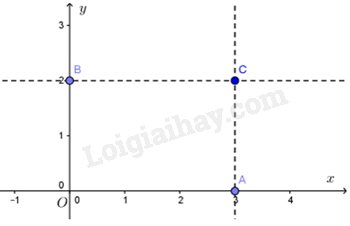
Gọi tên các giao điểm như hình vẽ, ta được hình chữ nhật OBCA.

Do đó, diện tích hình chữ nhật OBCA là: \({S_{OBCA}} = OA.OB = 3.2 = 6\) (đvdt)