Đề bài
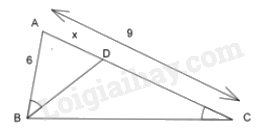
Cho hình bên biết \({\rm{AB}} = 6{\rm{\;cm}},{\rm{AC}} = 9{\rm{\;cm}},\widehat {ABD} = \widehat {BCA}\). Thế thì độ dài \({\rm{AD}}\) là:
-
A.
\(2{\rm{\;cm}}\)
-
B.
\(3{\rm{\;cm}}\)
-
C.
\(4{\rm{\;cm}}\)
-
D.
\(5{\rm{\;cm}}\)
Phương pháp giải
- Từ dữ kiện đã có chứng minh được 2 tam giác đồng dạng theo trường hợp góc - góc.
- Từ đó ta rút ra được tỉ lệ thức phù hợp, tính ra giá trị của .
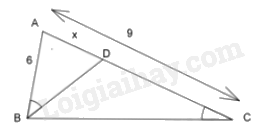
Xét \(\Delta ABD\) và \(\Delta ACB\) có:
\(\widehat A\) chung
\(\widehat {ABD} = \widehat {BCA}\left( {gt} \right)\)
Suy ra $\Delta ABD\backsim \Delta ACB\left( g-g \right)$
Suy ra \(\frac{{AB}}{{AC}} = \frac{{AD}}{{AB}}\)
\(\begin{array}{l}\frac{6}{9} = \frac{x}{6}\\x = \frac{{6.6}}{9} = 4{\rm{\;cm}}\end{array}\)
Đáp án C.
Đáp án : C