Cho hình bình hành ABCD AC > AB. Gọi E là hình chiếu của C — Không quảng cáo

Phương pháp giải

Sử dụng kiến thức trường hợp đồng dạng thứ ba của tam giác vuông: Nếu tam vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.

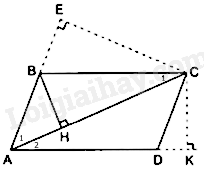
Tam giác AHB và tam giác AEC có: \(\widehat {{A_1}}chung,\widehat {AHB} = \widehat E = {90^0}\)

Do đó, \(\Delta AHB \backsim \Delta AEC \Rightarrow \frac{{AH}}{{AE}} = \frac{{AB}}{{AC}} \Rightarrow AB.AE = AC.AH\)

Vì BC// AD (do ABCD là hình bình hành) nên \(\widehat {{C_1}} = \widehat {{A_2}}\) , mà \(\widehat {BHC} = \widehat K = {90^0}\)

Do đó, \(\Delta AKC \backsim \Delta CHB \Rightarrow \frac{{AK}}{{CH}} = \frac{{AC}}{{CB}} \Rightarrow AK.CB = AC.CH\)

Vì ABCD là hình bình hành nên \(BC = AD\)

Do đó, \(AD.AK = AC.CH\left( 3 \right)\)

Từ (1), (2) và (3) ta có:

\(AB.AE + AD.AK = AC\left( {AH + CH} \right) = A{C^2}\)