Cho hình bình hành ABCD có AB = a = 12,5cm,BC = b = 7,25cm — Không quảng cáo

Phương pháp giải

Sử dụng kiến thức về tính chất đường phân giác của tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn thẳng ấy.

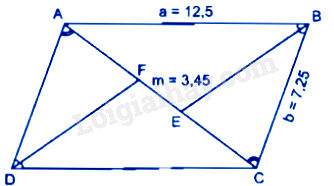
Vì ABCD là hình bình hành nên $\widehat {ABC} = \widehat {ADC}.$

Vì BE và DF lần lượt là phân giác của góc ABC và góc ADC nên $\widehat {ADF} = \widehat {CBE}$

Mặt khác, ta có: $AD = CB = b,\widehat {DAF} = \widehat {BCE}$ (so le trong)

Suy ra: $\Delta ADF = \Delta CBE\left( {g.c.g} \right)$ nên $AF = CE$

Đặt $AF = CE = x$

Xét tam giác ABC có BE là đường phân giác của góc ABC nên

$\frac{{AB}}{{BC}} = \frac{{AE}}{{CE}} = \frac{{FA + FE}}{{CE}} \Rightarrow \frac{a}{b} = \frac{{x + m}}{x} \Rightarrow x = \frac{{mb}}{{a - b}}$

$AC = 2x + m = \frac{{2mb}}{{a - b}} + m = \frac{{m\left( {a + b} \right)}}{{a - b}} = \frac{{3,45\left( {12,5 + 7,25} \right)}}{{12,5 - 7,25}} \approx 12,98cm$