Cho hình bình hành ABCD có I là giao điểm hai đường chéo — Không quảng cáo

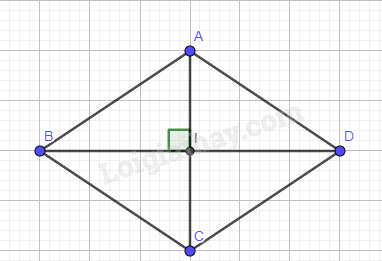
Theo tính chất hình bình hành ta có: I là trung điểm của AC và BD.

Suy ra:

\(\begin{array}{l}AI = \frac{1}{2}AC = \frac{1}{2}.6 = 3cm\\DI = \frac{1}{2}B{\rm{D}} = \frac{1}{2}.8 = 4cm\end{array}\)

Xét tam giác AID có: \(A{I^2} + I{{\rm{D}}^2} = A{{\rm{D}}^2}\left( {{3^2} + {4^2} = {5^2}} \right)\)

Suy ra: tam giác AID là tam giác vuông: AI ⊥ DI hay AC ⊥ BD

Hình bình hành ABCD có 2 đường chéo AC và BD vuông góc với nhau nên là hình thoi.

Suy ra: AB = BC = CD = DA = 5cm

Hai đường chéo của hình thoi cắt nhau tại trung điểm của mỗi đường.