Cho hình bình hành ABCD. Gọi E, F lần lượt là trung điểm — Không quảng cáo

Phương pháp giải

Chứng minh EPFQ là hình thoi từ đó suy ra số đo \(\widehat {ACD}\)

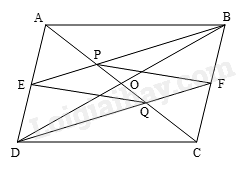
Gọi O là giao điểm của hai đường chéo AC và BD.

Vì ABCD là hình bình hành nên O là trung điểm của AC, BD và AD //CB, AD = BC

Xét tứ giác EDFB có ED // FB, \(ED = FB\left( { = \frac{1}{2}AD = \frac{1}{2}BC} \right)\).

Nên EDFB là hình bình hành.

Suy ra: BE = DF, BE // DF.

Xét \(\Delta ABD\)có P là giao điểm hai đường trung tuyến BE, AO nên P là trọng tâm

\(\Delta ABD \Rightarrow EP = \frac{1}{3}BE\).

Xét \(\Delta CBD\)có Q là giao điểm hai đường trung tuyến DF, CO nên Q là trọng tâm

\(\Delta CBD \Rightarrow QF = \frac{1}{3}DF\).

Mà BE = DF (cmt) \( \Rightarrow \)EP = QF.

Xét tứ giác EPFQ có \( \Rightarrow \)EP = QF, EP // QF \( \Rightarrow \)EPFQ là hình bình hành.

Để hình bình hành EPFQ là hình thoi thì \({\rm{EF}} \bot PQ\).

Mà EF // CD (do hình bình hành ABCD có AB //CD, E là trung điểm AD, F là trung điểm BC ).

Nên \(CD \bot PQ\) hay \(CD \bot AC \Rightarrow \widehat {ACD} = {90^0}\).