Cho hình bình hành ABCD.Trên đường chéo AC lấy điểm E sao cho AC = 3.AE. Qua E vẽ đường thẳng song song với CD cắt AD và BC theo thứ tự ở M và N. Cho các khẳng định sau:
\((I)\Delta AME \backsim \Delta A{\rm{D}}C\) , tỉ số đồng dạng \({k_1} = \frac{1}{3}\)
\((II)\Delta CBA \backsim \Delta A{\rm{D}}C\) , tỉ số đồng dạng \({k_2} = 1\)
\((III)\Delta CNE \backsim \Delta A{\rm{D}}C\) , tỉ số đồng dạng \({k_3} = \frac{2}{3}\)
Chọn câu đúng:
-
A.
( I ) đúng, ( II ) và ( III ) sai.
-
B.
( I ) và ( II ) đúng, ( III ) sai.
-
C.
( I ) , ( II ), ( III ) đều đúng.
-
D.
( I ), ( II ), ( III ) đều sai.
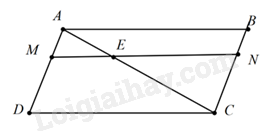
Xét \(\Delta A{\rm{D}}C\) có \(ME//C{\rm{D}}\) (gt) \( \Rightarrow \Delta AM{\rm{E}} \backsim \Delta A{\rm{D}}C(1)\) theo tỉ số đồng dạng \({k_1} = \frac{{A{\rm{E}}}}{{AC}} = \frac{1}{3}\)
Vì ABCD là hình bình hành nên
+ \(\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over B} = \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over D} \)
+ \(AB//C{\rm{D}} \Rightarrow \widehat {BAC} = \widehat {AC{\rm{D}}}\) (so le trong)
+ \(AD//BC \Rightarrow \widehat {ACB} = \widehat {CA{\rm{D}}}\) (so le trong)
+ AD = BC ; AB = CD
Xét \(\Delta CBA\) và \(\Delta A{\rm{D}}C\) có :
+ \(\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over B} = \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over D} ;\widehat {BAC} = \widehat {AC{\rm{D}}};\widehat {ACB} = \widehat {CA{\rm{D}}}(cmt)\)
+ \(\frac{{AB}}{{C{\rm{D}}}} = \frac{{BC}}{{A{\rm{D}}}} = \frac{{AC}}{{AC}}( = 1)\)
\( \Rightarrow \Delta CBA \backsim \Delta A{\rm{D}}C\) theo tỉ lệ đồng dạng \({k_2} = 1\)
Xét \(\Delta ABC\) có :
EN//CD (gt) mà AB//CD (cmt)
\( \Rightarrow EN//AB \Rightarrow \Delta CNE \backsim \Delta CBA\)
Mà \(\Delta CBA \backsim \Delta A{\rm{D}}C(cmt)\)
\( \Rightarrow \Delta CNE \backsim \Delta A{\rm{D}}C\) theo tỉ lệ đồng dạng \({k_3} = \frac{{CE}}{{AC}} = \frac{2}{3}\) (Vì \(AC = 3{\rm{AE}} \Rightarrow CE = \frac{2}{3}AC)\)
Vậy khẳng định (I), (II), (III) đều đúng.
Đáp án : C