Cho hình chóp S. ABC có ABC là tam giác cân tại C, SA vuông — Không quảng cáo

Phương pháp giải

+ Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì $d \bot \left( P \right)$.

+ Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.

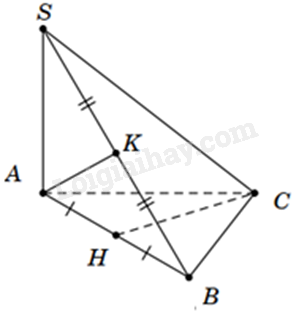
Vì H là trung điểm của AB, mà tam giác ABC cân tại C nên $CH \bot AB$.

Ta có: $SA \bot \left( {ABC} \right),CH \subset \left( {ABC} \right) \Rightarrow SA \bot CH$

Ta có: $CH \bot AB$, $SA \bot CH$, SA và AB cắt nhau tại A và nằm trong mặt phẳng (SAB) nên $CH \bot \left( {SAB} \right)$. Mà $AK,SB \subset \left( {SAB} \right) \Rightarrow AK \bot CH,SB \bot CH$

Do đó, đáp án sai là D.

Đáp án D.