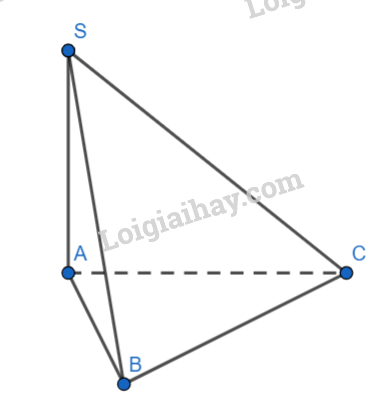
Cho hình chóp S. ABC có đáy ABC là tam giác vuông tại B và — Không quảng cáo

Phương pháp giải

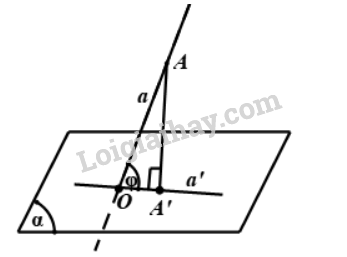
Bước 1: Tìm giao điểm O của đường thẳng a và $(\alpha )$

Bước 2: Xác định hình chiếu A’ của điểm A xuống $(\alpha )$

Bước 3: Suy ra: $\left( {AO,(\alpha )} \right) = \left( {AO,A'O} \right) = \widehat {AOA'}$

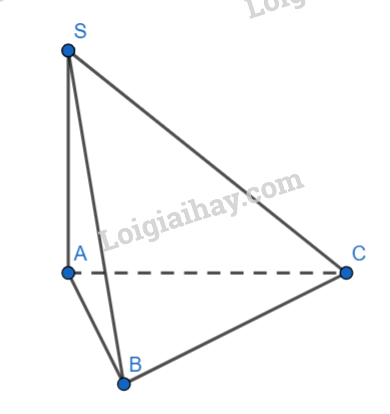
Do $SA \bot (ABC)$nên A là hình chiếu của S lên (ABC)

Ta có: $\left( {SB,(ABC)} \right) = (SB,AB)$

Xét $\Delta SAB$ vuông tại A có:

$\begin{array}{l}\tan \left( {SB,AB} \right) = \tan \widehat {SBA} = \frac{{SA}}{{AB}} = \frac{{\sqrt {S{B^2} - A{B^2}} }}{{AB}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3 \\ \Rightarrow \widehat {SBA} = {60^0}\end{array}$

Đáp án B.