Cho hình chóp S. ABC có SA ⊥ ABC, SA = h. Gọi M, N, P tương — Không quảng cáo

a) \(d((MNP),(ABC)) = h\)

b) \(d(NP,(ABC)) = \frac{h}{2}\)

c) \(d(A,(SBC)) = \frac{{ah}}{{\sqrt {{a^2} + {h^2}} }}\)

d) \((MNP)//(ABC)\)

Sử dụng phương pháp tính khoảng cách từ điểm đến mặt phẳng và khoảng cách từ đường thẳng đến mặt phẳng

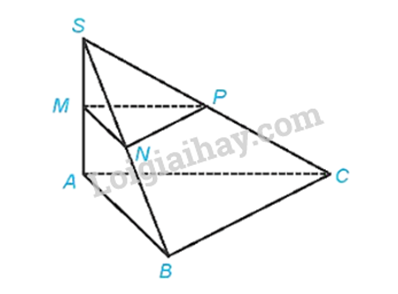
a) Xét tam giác SAB có M là trung điểm của SA, N là trung điểm của SB nên MN là đường trung bình của tam giác SAB. Suy ra \(MN//AB\),do đó \(MN//(ABC)\)

Xét tam giác SBC có N là trung điểm của SB, P là trung điểm của SC nên PN là đường trung bình của tam giác SBC. Suy ra \(PN//BC\),do đó \(PN//(ABC)\)

Khi đó, \(d((MNP),(ABC)) = d(M,(ABC))\)

Vì \(SA \bot (ABC)\) nên \(MA \bot (ABC)\). Do đó \(d(M,(ABC)) = MA\)

Vì M là trung điểm SA nên \(AM = \frac{{SA}}{2} = \frac{h}{2}\)

Do đó \(d((MNP),(ABC)) = \frac{h}{2}\)

b) Vì \(PN//(ABC)\) nên \(d(NP,(ABC)) = d(N,(ABC))\)

Vì \(MN//(ABC)\) nên \(d(N,(ABC)) = d(M,(ABC)) = MA = \frac{h}{2}\)

Vậy \(d(N,(ABC)) = \frac{h}{2}\)

c) Vì tam giác ABC là tam giác vuông tại B nên \(BC \bot AB\)

Vì \(SA \bot (ABC)\) nên \(SA \bot BC\)mà \(BC \bot AB\) nên \(BC \bot (SAB)\), suy ra \((SBC) \bot (SAB)\)

Kẻ \(AH \bot SB\) tại H

Vì \(\left\{ \begin{array}{l}(SBC) \bot (SAB)\\(SBC) \cap (SAB) = SB\\AH \subset (SAB)\\AH \bot SB\end{array} \right. \Rightarrow AH \bot (SBC)\)

Khi đó \(d(A,(SBC)) = AH\)\(\)

Vì \(SA \bot (SBC)\) nên \(SA \bot AB\)

Xét tam giác SAB vuông tại A, AH là đường cao, có:

\(\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{B^2}}} = \frac{1}{{{h^2}}} + \frac{1}{{{a^2}}} = \frac{{{a^2} + {h^2}}}{{{a^2}{h^2}}} \Rightarrow AH = \frac{{ah}}{{\sqrt {{a^2} + {h^2}} }}\)

Vậy \(d(A,(SBC)) = \frac{{ah}}{{\sqrt {{a^2} + {h^2}} }}\)

d)\(MN//(ABC)\) mà \(MN \subset (MNP) \Rightarrow (MNP)//(ABC)\)