Đề bài
Cho hình chóp S.ABC có SA ⊥ (ABC) và ΔABC vuông ở B . AH là đường cao của ΔSAB . Khẳng định nào sau đây sai ?
-
A.
\(SA \bot BC\)
-
B.
\(AH \bot BC\)
-
C.
\(AH \bot AC\)
-
D.
\(AH \bot SC\)
Phương pháp giải
Sử dụng định lý đường vuông góc với mặt phẳng
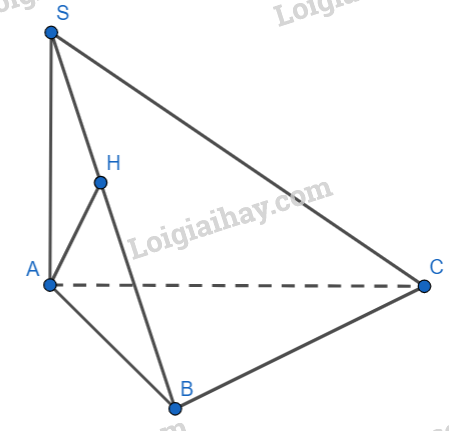
Đáp án B,D.
Ta có: \(\left\{ \begin{array}{l}BC \bot BA\\BC \bot SA\\SA,BA \subset (SAB)\\SA \cap BA\end{array} \right. \Rightarrow BC \bot (SAB) \Rightarrow BC \bot AH\)
Mặt khác:
\(\begin{array}{l}\left\{ \begin{array}{l}AH \bot BC\\AH \bot SB\\SB,BC \subset (SBC)\\SB \cap BC\end{array} \right. \Rightarrow AH \bot (SBC)\\ \Rightarrow AH \bot BC;\,AH \bot SC\end{array}\)
Đáp án A: \(SA \bot (ABCD) \Rightarrow SA \bot BC\)
Đáp án C.
Đáp án : C