Cho hình chóp S. ABCD có ABCD là hình vuông cạnh bằng a và các cạnh bên đều bằng a. Gọi M, N lần lượt là trung điểm của AD, SD. Góc giữa hai đường thẳng MN và SC bằng:
-
A.
\({90^0}\).
-
B.
\({60^0}\).
-
C.
\({30^0}\).
-
D.
\({70^0}\).
Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm O và lần lượt song song (hoặc trùng) với a và b; kí hiệu \(\left( {a,b} \right)\) hoặc \(\widehat {\left( {a;b} \right)}\).
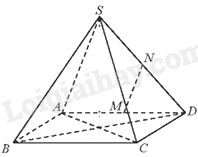
Vì M, N lần lượt là trung điểm của AD, SD nên MN là đường trung bình của tam giác SAD. Do đó, MN//AS. Suy ra, \(\left( {MN,SC} \right) = \left( {SA,SC} \right) = \widehat {SAC}\).
Vì tam giác ABC vuông tại B nên \(A{C^2} = A{B^2} + B{C^2} = 2{a^2}\)
Vì \(A{C^2} = S{A^2} + A{C^2}\) nên tam giác SAC vuông tại S (định lí Pythagore đảo)
Do đó, \(\widehat {ASC} = {90^0}\). Vậy \(\left( {MN,SC} \right) = {90^0}\).
Đáp án A.
Đáp án : A