Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Gọi M — Không quảng cáo

Phương pháp giải

Sử dụng kiến thức về đường thẳng song song với mặt phẳng: Cho đường thẳng a song song với mặt phẳng (P). Nếu mặt phẳng (Q) chứa a và cắt (P) theo giao tuyến b thì a song song với b.

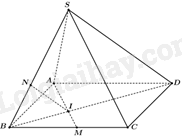
Tam giác ABC có hai đường trung tuyến BD và AM cắt nhau tại I nên I là trọng tâm của tam giác ABC.

Suy ra: $\frac{{BI}}{{BD}} = \frac{1}{3} \Rightarrow \frac{{ID}}{{BD}} = \frac{2}{3}$

Vì $\left( \alpha  \right)$ và mặt phẳng (SBD) có điểm chung là I, $\left( \alpha  \right)$//SD, $SD \subset \left( {DBD} \right)$ nên giao tuyến của $\left( \alpha  \right)$ và mặt phẳng (SBD) là đường thẳng qua I song song với SD cắt SB tại N. Do đó, $\frac{{SN}}{{SB}} = \frac{{ID}}{{DB}} = \frac{2}{3}$