Cho hình chóp S. ABCD có đáy ABCD là hình bình hành tâm O — Không quảng cáo

a) Giao tuyến của hai mặt phẳng (SAB) và (SAD) là SO

b) SO thuộc mặt phẳng (SBD)

c) Gọi I là giao điểm của SC và (P). Khi đó OI//SA

d) Thiết diện giữa (P) và hình chóp là hình bình hành

Sử dụng các định lý về đường thẳng song song với mặt phẳng, cách tìm giao tuyến, thiết diện của hai mặt phẳng.

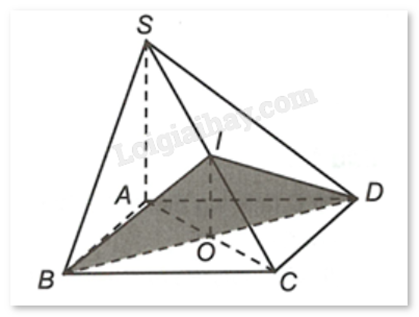
a) Sai . Giao tuyến của hai mặt phẳng (SAB) và (SAD) là SA.

b) Đúng . SO thuộc mặt phẳng (SBD) vì cả \(S \in (SBD)\), \(O \in BD \subset (SBD)\).

c) Đúng . Có \(OI \subset (P)\) mà SA//(P) nên SA không cắt đường thẳng nào trong (P), tức OI//SA (do OI, SA cùng thuộc mặt phẳng (SAC)).

d) Sai . Thiết diện là tam giác BID.