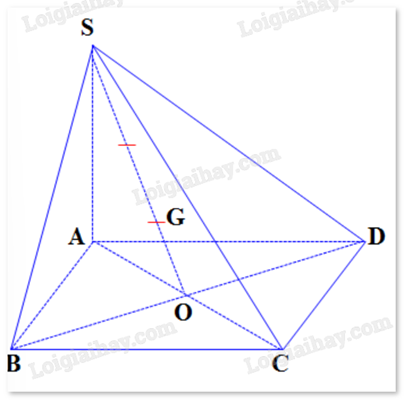
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O và G là trọng tâm tam giác SBD.
a) \(\overrightarrow {SG} = \frac{2}{3}\overrightarrow {SO} \)
b) \(\overrightarrow {AS} + \overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AG} \)
c) \(\overrightarrow {SA} + \overrightarrow {SC} = 3\overrightarrow {SG} \)
d) \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = 12\overrightarrow {GO} \)
a) \(\overrightarrow {SG} = \frac{2}{3}\overrightarrow {SO} \)
b) \(\overrightarrow {AS} + \overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AG} \)
c) \(\overrightarrow {SA} + \overrightarrow {SC} = 3\overrightarrow {SG} \)
d) \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = 12\overrightarrow {GO} \)
Sử dụng quy tắc cộng vecto, lý thuyết các vecto bằng nhau, vecto đối nhau, quy tắc trọng tâm.
a) Đúng. Vì hai vecto \(\overrightarrow {SG} \), \(\overrightarrow {SO} \) cùng hướng và \(\left| {\overrightarrow {SG} } \right| = \frac{2}{3}\left| {\overrightarrow {SO} } \right|\).
b) Sai. Vì \(\overrightarrow {AS} + \overrightarrow {AB} + \overrightarrow {AD} = 3\overrightarrow {AG} \) (quy tắc trọng tâm)
c) Đúng. Vì \(\overrightarrow {SA} + \overrightarrow {SC} = 2\overrightarrow {SO} = 2.\frac{2}{3}\overrightarrow {SG} = 3\overrightarrow {SG} \).
d) Đúng. Vì \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = \overrightarrow {SA} + \overrightarrow {SC} + \overrightarrow {SB} + \overrightarrow {SD} = 2\overrightarrow {SO} + 2\overrightarrow {SO} \)
\( = 4\overrightarrow {SO} = 4.3\overrightarrow {GO} = 12\overrightarrow {GO} \) .