Đề bài
Cho hình chóp S. ABCD có đáy ABCD là hình bình hành và \(\widehat {SAB} = {100^0}\). Góc giữa hai đường thẳng SA và CD bằng bao nhiêu độ?
-
A.
\({100^0}\).
-
B.
\({90^0}\).
-
C.
\({80^0}\).
-
D.
\({70^0}\).
Phương pháp giải
+ Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm O và lần lượt song song (hoặc trùng) với a và b, kí hiệu \(\left( {a,b} \right)\) hoặc \(\widehat {\left( {a;b} \right)}\).
+ Góc giữa hai đường thẳng không vượt quá \({90^0}\).
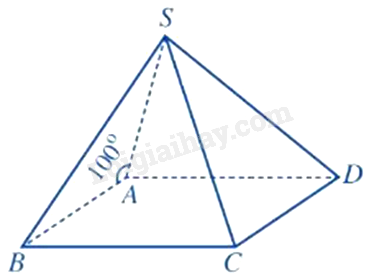
Vì ABCD là hình bình hành nên \(AB//CD\)
Do đó, \(\left( {SA,CD} \right) = \left( {SA,AB} \right) = {180^0} - \widehat {SAB} = {80^0}\)
Đáp án : C