Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, \(AB = 2a,AD = a,\Delta SAD\) đều và nằm trong mặt phẳng vuông góc với mặt đáy. Gọi \(\varphi \) là góc phẳng nhị diện \(\left[ {S,BC,A} \right]\). Khẳng định nào sau đây là đúng?
-
A.
\(\varphi {\rm{ \;}} = 60^\circ \).
-
B.
\({\rm{tan}}\varphi {\rm{ \;}} = \frac{{\sqrt 3 }}{4}\).
-
C.
\(\varphi {\rm{ \;}} = 30^\circ \).
-
D.
\({\rm{tan}}\varphi {\rm{ \;}} = \frac{{\sqrt 3 }}{2}\).
Xác định góc giữa hai mặt phẳng tạo thành.
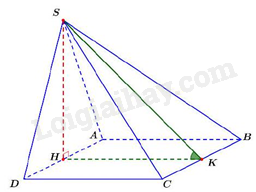
Suy ra \(SH \bot \left( {ABCD} \right)\) và \(HK \bot BC\).
Khi đó: \(\left\{ {\begin{array}{*{20}{l}}{BC \bot HK}\\{BC \bot SH}\end{array} \Rightarrow BC \bot \left( {SHK} \right) \Rightarrow BC \bot SK} \right.\).
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{\left( {SBC} \right) \cap \left( {ABC} \right) = BC}\\{HK \bot BC}\\{SK \bot BC}\end{array}\; \Rightarrow \left[ {S,BC,A} \right] = \widehat {SKH} = \varphi } \right.\).
Xét vuông tại \(H\), ta có:
\({\rm{tan}}\varphi {\rm{ \;}} = {\rm{tan}}\widehat {SKH} = \frac{{SH}}{{HK}} = \sqrt 3 {\rm{ \;}} \Rightarrow \varphi {\rm{ \;}} = 60^\circ \).
Đáp án A.
Đáp án : A